粒子径について

前回の記事で取り上げた腸溶性錠剤に関する特許明細書の中に「平均粒子径」や「メジアン径」という言葉が出てきました。
「該タルクは好ましくは微粒子グレードのもの、具体的には、平均粒子径（体積平均粒子径；メジアン径Ｄ５０）が、０．１μｍ～１５μｍのもの、を用いる。」

そこで今回は粒子径について書いてみました。

粒子径を測る意味

粒子の大きさは数ナノメートルから数ミリメートルまでとかなりの幅がありますが、個々の粒子の大きさを表す基準となる長さが「粒子径」です。
粒子径の求め方は後述しますが、なぜ粒子の大きさを求めることが必要になるのでしょうか。

それは、粒子は大きさによって、流動性、溶解性、光の散乱・吸収特性、沈降速度、反応性、扱いやすさ、などが変わるためです。

例えば、食品に使われる素材は粒子の大きさによって、ざらざらしている、なめらかである、など食感が変わります。

加工プロセスでは、あまりにも粒子のサイズが小さいと加工中に飛散しやすくなり、作業員の肺に吸引されて身体に影響を及ぼすこともあります。

また、塗料などとして粒子を液体中に分散させて用いる場合や薬剤の吸収効率を考える場合には、溶解度や反応性と流動性のバランスを考える必要があります。
一定量の材料を比較したとき、粒子が小さいほど全体としての表面積が大きくなるので、一般的に粒子径が小さいほど反応性や溶解度が高くなります。
しかし、粒子径が小さくなると粒子同士の間に働くファンデルワールス力などの分子間力も大きくなるため、流動性が減少します。

化粧品などでは、粒子のサイズによって光の反射や屈折の仕方が変わることを利用して、製品による光沢の差を生み出しています。

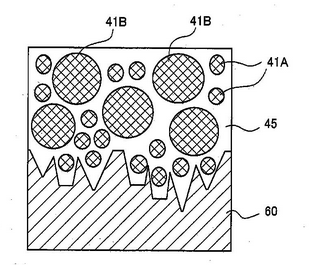
接着層や表面塗装では、下図のような凸凹のある表面を考えたときに、先に小さな粒子を使って細かい溝を埋め、その上に大きな粒子の層を作ることで水平な層を作る、ということも考えられます。

粒子径の種類

では、粒子径はどのように定義するのでしょうか。

粒子が完全な球状（真球）であれば直径によって粒子の大きさの比較が可能ですが、実際の粒子は真球に近いものからいびつな非球状のものまで様々です。

粒子径の求め方は、大きく次のように分類できます。

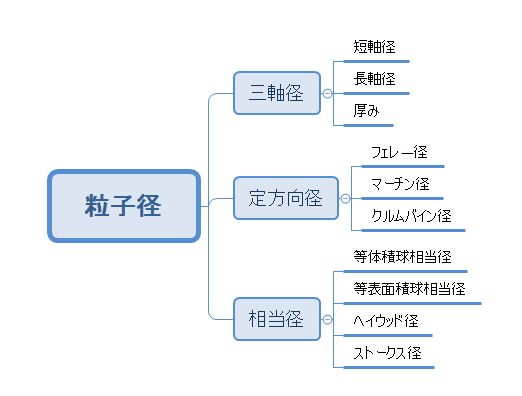
これらのうちどれが一番正確か、ということではなく、粒子を扱う際の目的に応じてそれぞれの基準を使い分けることが重要になります。

では、それぞれの粒子径基準について見ていきましょう。

三軸径

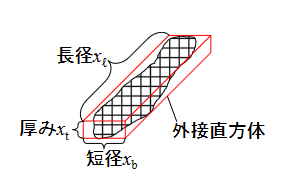
いびつな粒子はそのままでは大きさを定義することは困難ですが、そのような粒子に外接する最も小さい平行六面体を考えることで長さを定義することが可能になります。
外接する平行六面体のそれぞれの辺（短軸径、長軸径、厚み）の長さを粒子径とします。

定方向径

３次元の粒子に光を当ててその影を投影してできる平面上の投影図を用いて、一定の方向に沿って測定した長さを粒子径とするものです。
顕微鏡が画像分析装置で計測されます。

定方向径には以下のような種類があります。

フェレー径

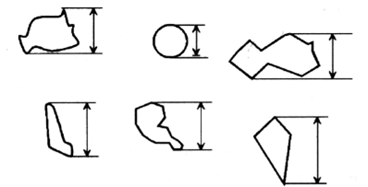
粒子に平行に外接する２本の直線の間の距離をフェレー径といいます。
選ぶ場所によってフェレー径も色々な長さが考えられますが、通常はフェレー径が最大となる長さを粒子径とします。

マーチン径

投影面積を二等分する線分の長さを粒子径とします。

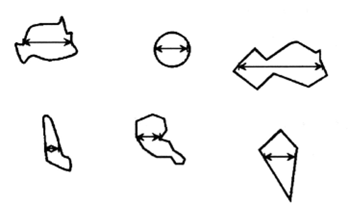
クルムバイン径

定方向で最大幅となる箇所の長さを粒子径とします。

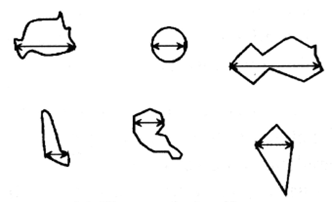
相当径

球状であればどこを測っても同じ直径という基準で測れますが、球状以外であれば測る部分により大きさが変わります。
そこで、非球状の粒子を何らかの方法で球（または円）に換算して、その球（または円）の直径を使って表したものが相当径です。

どのような方法で球（または円）に換算するかによって、相当径には次のような種類があります。

等体積球相当径

非球状の粒子と同体積の球を想定し、その球の直径を粒子径とするものです。

等表面積球相当径

非球状の粒子の表面積と同じ表面積をもつ球を想定し、その直径を粒子径とするものです。

ヘイウッド径

非球状の粒子の投影面積と同じ面積をもつ円を想定し、その直径を粒子径とするものです。

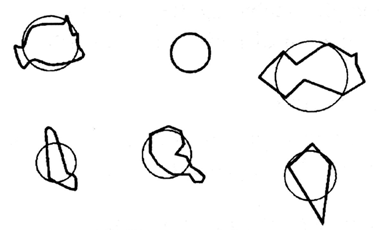
ストークス径

非球状の粒子と同じ沈降速度をもつ球を想定し、その球の直径を粒子径とするものです。

以上のように、すべての粒子が球状であるという仮定の下に球相当径を使うことで、粒子の大きさを直径という一つの統一された基準で議論することが可能になります。
ただし、個々の粒子のアスペクト比（直径と短径の縦横の比）が非常に高い針状の粒子などは球形で考えることが不都合になる場合もあるので別途考慮する必要があります。

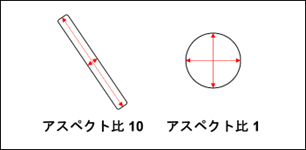
粒度分布

これまで1つ1つの粒子の大きさをどのように計測するか、ということを見てきました。
しかし、製品加工において粒状の材料を扱う際に個々の粒子を一つずつ取り出して扱うようなことはなく、通常は一定量の粒子を一度に扱うことになります。
私たちが普段料理をするときに小麦粉の粒を一粒ずつ取り出すというようなことをせず一定量を取り出して使うのと同じです。

その一定量の中には多数の粒子が存在することになりますが、どの粒子径の粒子がどれだけ存在するか、という分布を考える必要があります。

そこで粒子径ごとの粒子の頻度（存在量）を表したものが粒度分布で、ヒストグラムを用いたグラフで表されます。
粒度分布を考えるうえで、重要となる3つの代表値があります。
以下の3つです。
　
　・モード径（最頻径）
　・メジアン径（中央径）
　・平均径　

モード径

粒度分布の最頻値を取る粒子径をモード径といいます。
調査対象の中で粒子径がモード径と同じになる粒子が最も多く存在するということを示します。

メジアン径

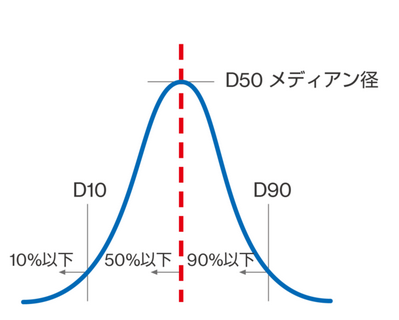
粒子全体のうち、半分がこの粒子径より小さく、残りの半分がこの粒子径より大きくなるような、中央の値のことをメジアン径といいます。
メジアン径を境に、それより小さいものが50％あるということになるので、D50と表します。

メジアン径はD50ですが、D90であればその粒子径よりも小さいものが全体の90％を占めるような粒子径を指し、Ｄ10であればその粒子径よりも小さいものが全体の10％を占めるような粒子径を指します。

平均径

平均となる粒子径です。
平均と一口に言っても、算術平均、幾何平均、加重平均、調和平均、など様々な求め方があります。

平均径について、よく使われるのは次の3つです。

　・算術平均径　
　・表面積平均径
　・体積平均径

D1、D2、D3・・・Diの粒子径の粒子がそれぞれN1、N2、N3・・・Ni個ずつあったとすると、それぞれ下図の計算式で表されます。

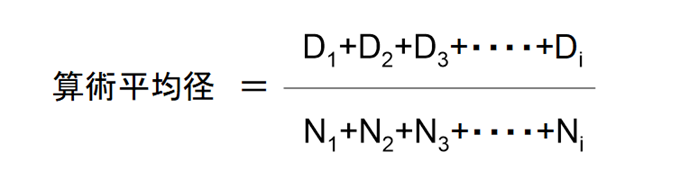
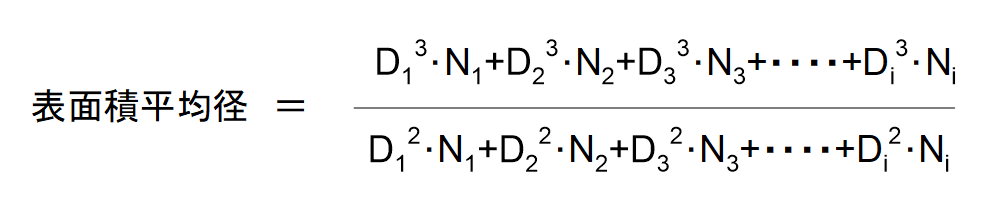
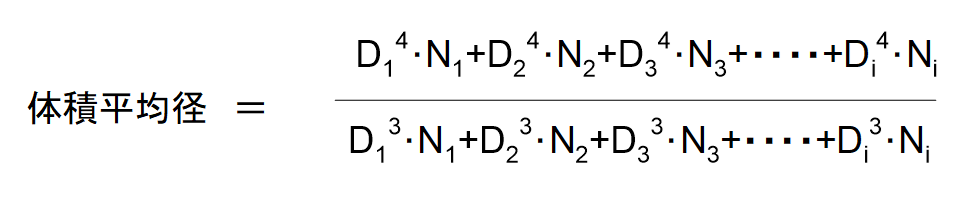
算術平均は単純な平均値ですが、表面積平均と体積平均は加重平均になっています。

算術平均と加重平均の違いについて例を使って確認しましょう。
例えば次のような商品を売っているお店があったとして、商品の平均の値段がいくらか考えます。

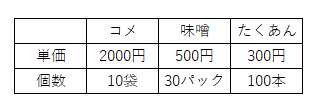
算術平均で求める場合は、単純に3つの商品の単価を足して3で割ればよいので、次の式で求めます。
（2000+500+300）÷ 3 ≒ 933
よって、平均933円です。

加重平均で求める場合は、それぞれの商品が何個あるかによって重みづけをするため、次のように求めます。
（2000×10　+　500×30　＋　300×100）÷（10＋30＋100）≒ 464
よって、平均464円です。

球の表面積は直径の２乗に比例、体積は直径の３乗に比例することから、
表面積平均は直径の２乗で重みづけ、体積平均径は直径の3乗で重みづけした値になっています。

これらのうち、どの平均径が使われるかは、粒度分布の基準によって異なります。その点は後述します。

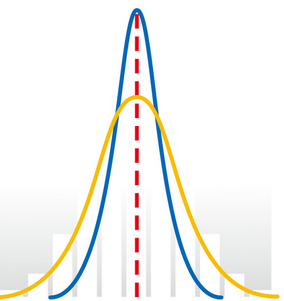
分布が対照的であれば、モード径・メジアン径・平均径の値はほぼ等しくなりますが、分布が非対称であればそれぞれの値は異なります。

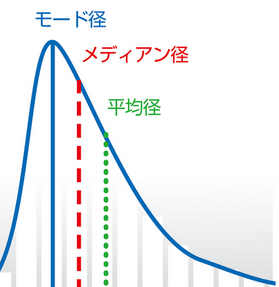
このように見てくると、腸溶性錠剤に関する特許に出てきた以下の表現は、平均径＝メジアン径としているので厳密には不正確ということになります。

「該タルクは好ましくは微粒子グレードのもの、具体的には、平均粒子径（体積平均粒子径；メジアン径Ｄ５０）が、０．１μｍ～１５μｍのもの、を用いる。」

ただし、平均径とメジアン径が近似できる場合、簡便性の面から累積の50%粒子径をもって平均径と呼ばれる場合がよくあるようなので、今回はこの場合に該当するのだと思われます。

平均粒子径、モード径、メジアン径を意識して区別している例としては、以下の特許が見つかりました。

研磨用スラリーに関する特許（特開2021-107479）

【請求項１】
樹脂を含む被研磨物を研磨する研磨用スラリーであって、
アルミナ砥粒と、シリカ砥粒とを含有し、
前記シリカ砥粒は、コロイダルシリカの複数の１次粒子で構成された凝集粒子を含み、
前記１次粒子の平均粒子径が前記アルミナ砥粒のメジアン径よりも小さい、研磨用スラリー。

アルミナはシリカに比べて硬く研削力に優れる。
よって、斯かる研磨用スラリーは、アルミナ砥粒を含有することにより、研磨レートを高めることができる。
また、斯かる研磨用スラリーは、コロイダルシリカの複数の１次粒子で構成された凝集粒子を含有することにより、該凝集粒子によりアルミナ砥粒の転がりを規制しやすくなり、その結果、アルミナ砥粒の優れた研削力を発揮しやすくなる。
さらに、斯かる研磨用スラリーは、１次粒子の平均粒子径が、前記アルミナ砥粒のメジアン径よりも小さいことにより、該凝集粒子によるアルミナ砥粒の転がりの規制をより一層発揮しやすくなる。
従って、本実施形態に係る研磨用スラリーは、樹脂を含む被研磨物の研磨における研磨レートを高め得る。

この特許は、アルミナ砥粒とシリカ砥粒を併用した研磨用スラリーに関する特許です。
スラリーとは、液体中に固体粒子が分散して懸濁液となった状態を言います。

研磨用のスラリーを被研磨物に塗布してこすると、分散質である粒子が摩擦等の物理的な作用、あるいは化学反応によって、被研磨物を研磨します。
研磨工具では深い傷をつける恐れがあるような場合でも、分散質が適度に被研磨物の表面を転がることで深い傷がつきにくくなり、また均一に広がって研磨効率を上げます。
しかし、過度に転がりすぎると砥粒が被研磨物の表面から逃げていってうまく研磨できません。

アルミナ砥粒は研削力に優れていますが必要以上に転がりやすいという問題があります。
そのため、この特許ではシリカ砥粒を併用し、シリカ砥粒が凝集してできる粒子がアルミナ砥粒を取り囲んで転がりを規制するようにしています。
その際、シリカ砥粒の凝集前の粒子径が小さいほど表面積が大きくなるので、凝集してできる二次粒子がアルミナ砥粒と作用しやすくなり、転がり規制の効果を発揮できるということかと思います。

なぜシリカ砥粒では平均粒子径を使いアルミナ砥粒ではメジアン径を使うのか、という点は明細書には明記されていませんでしたが、両者の粒度分布に違いがあるためだと思われます。
平均粒子径を使った場合は粒子の全体的な傾向が反映されるのに対して、メジアン径は極端に粒子径の異なる値を反映しにくくなるということが考えられます。

ドーナツ用米粉に関する特許（特開2023-102399）

本発明のドーナツ用米粉は、体積基準のメジアン径（Ｄ５０）が６５～６００μｍであり、体積基準のモード径（Ｍ）を体積基準のメジアン径で除した値（Ｍ／Ｄ５０）が１．５以下である。前記範囲を満たす米粉を用いると、ザクザク感があり口どけが良く、油ちょう後に保存しても食感が劣化し難いドーナツを得ることができる。更に、冷凍保存した後に常温解凍しても、ザクザク感があり口どけのよい食感が劣化されがたいドーナツを得ることができる。

なぜＭ／Ｄ５０が１．５以下だとそのような効果が得られるのかについて具体的な説明は書かれていませんでしたが、モード径とメジアン径の差を近づけることで粒度分布が比較的均一になるため、調理工程で生地がしっかりと混ざりやすくなり、食感のムラや劣化を防げるのではないかと想像します。

粒度分布の基準

粒度分布の横軸は粒子径で表せますが、縦軸は何を基準にするかによって変わってきます。

個数基準

個数基準は、個々の粒子径における表面積や体積の影響を捨象して、粒子の個数を基準に粒度分布を表したものです。
細かい粒子も大きな粒子も同じく1つの粒子として数えるため、体積で考えると影響の無視されやすい微粒子の個数を算出したい場合に適しています。
バイオ・メディカル系の分野でよく使われます。

先述の通り、平均径には主に算術平均径、表面積平均径、体積平均径、の３種類がありましたが、個数基準を用いた場合の平均径は算術平均径となります。

体積基準

体積基準は、粒子径における体積の違いを考慮し、体積を縦軸に取って表したものです。
例えば、同じ３個でもビー玉が３個あるのとゴルフボールが３個あるのとでは体積が全く異なります。
体積基準では大きな粒子ほど粒度分布に影響が出やすいため、粗大粒子の検出が重要になる場合に適しています。

体積基準を使って粒度分布を表した場合の平均径には体積平均径を使うことになります。

表面積基準

表面積基準は、個々の粒子径における面積に基づいて粒度分布を表したものです。
表面積基準を使って粒度分布を表した場合の平均径には表面積平均径を使うことになります。

一般的には粒度分布は個数基準か体積基準で表されるので、あまり使用例はないようです。
特許を検索してもほとんど見つかりませんでした。

下図は同じサンプルについて、水色のグラフで個数基準を、青色のグラフで体積基準をそれぞれ表したものです。
同じサンプルを使っていても個数基準と体積基準が変われば粒度分布が異なることが分かります。

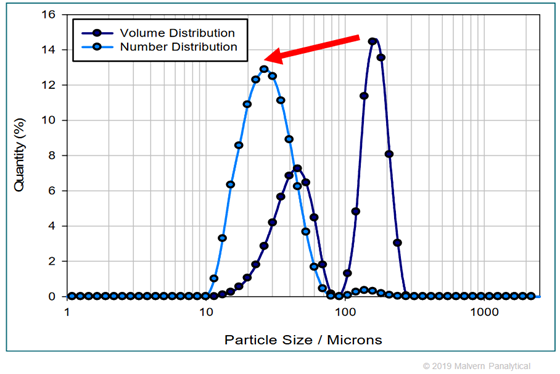
どのような基準に基づいて粒子径を算出しているかという点は非常に重要です。

ある基準に基づいて平均粒子径の範囲を指定したとしても、別の基準から算出した平均粒子径ではその範囲に収まらないということが考えられます。
どのような基準で平均粒子径を算出しているのかが不明確であったために特許が取消になった例もあります。
（平成 15年 (行ケ) 272号 特許取消決定取消請求事件）

参考）
HORIBA Scientific “粒子径とは” https://www.horiba.com/jpn/scientific/technologies/particle-characterization-jp/particle-size-jp/what-is-particle-size-jp/（参照2024-08-10）
島津製作所 ”粉博士のやさしい粉講座” https://www.an.shimadzu.co.jp/service-support/technical-support/analysis-basics/powder/lecture/beginner/index.html（参照2024-08-11）
マイクロトラック・ベル ”粒子径測定における体積平均径[MV]とはどのような粒子径か？” https://www.microtrac.com/jp/applications/knowledge-base/volume-average-particle-size/（参照2024-08-11）
マルバーン・パナリティカル “ウェブセミナー～はじめての粒度分布～” https://www.materials-talks.jp/files/20190513112749_0.pdf（参照2024-08-11）
SK弁理士法人 “「平均粒径」という用語を使うときは注意が必要” https://skiplaw.jp/%E6%97%A5%E6%9C%AC%E3%80%80%E6%98%8E%E7%B4%B0%E6%9B%B8/4979/（参照2024-08-11）

8/9（金）学習時間：4.5H
・岡野の化学（194）（195）
・腸溶性錠剤に関する特許に出てきた化合物の構造式や性質を調べる（途中まで）
その他）
・2558　NaHCO3について
・2697、3954　受講生ブログへのコメント

8/10（土）学習時間：7.5H
・岡野の化学（196）～（198）
・腸溶性のカプセル錠に関する特許の全体を読んで分からない部分をチェック
・相転移と相変化の違いについて
その他）
・0626　類似語をどう切り分けるか
・0568　Just Right 活用術

8/11（日）学習時間：13H
・粒子径について調べてまとめ
・ドーナツ粉に関する特許と研磨用スラリーに関する特許の内容をざっと確認
課題）
・腸溶性錠剤に関する特許に出てきた化合物の構造式や性質を調べる（続き）
・腸溶性のカプセル錠に関する特許の続き
・研磨用スラリーに関する特許を詳細に読む
その他）
・4037　統計学の学び方
・1132　夢子マインドとトライアル