理想気体について

岡野の化学で理想気体について学習したので、今回はその内容のまとめと、参照した特許について少し書いてみました。

理想気体とは

現実に存在する気体を実在気体と呼びます。
それに対して、現実には存在しないけれども、最も望ましい状態の気体を理想気体と呼びます。

なぜ理想気体というものを考えるのでしょうか？
実在気体について議論しようとすると、色々な細かな条件を考慮しなければならず、議論が非常に複雑になってしまいます。
そのため、個々の気体における細かな違いを無視して単純なモデルとすることで、大部分に共通する気体の基本的な性質を議論するのです。
こうすることで初めて、ボイル・シャルルの法則などの公式に当てはめて考えられるようになります。

具体的には、次の3つの条件で理想気体を考えます。
　①分子自体の体積をないものとする
　②分子間力が生じないものとする
　③高圧・低温の条件でも気体状態のままであるとする

①分子自体の体積をないものとする

実際にはもちろん分子が存在する以上、分子にもそれ自体の体積があります。
しかし、分子の種類によってそれぞれ異なる体積を考慮するのは非常に大変なため、一律で分子自体の体積を0とします。

ここで分子の体積を0にしたからといって、気体の体積が0になるわけではありません。
前回の記事で自由体積という考え方について書きましたが、
分子自体の体積と分子が動き回れる空間の体積とを合わせて気体の体積、と言っているので、分子自体の体積が0だからといって気体の体積も0になるということはないのです。

②分子間力が生じないものとする

実際には分子間には様々な力が働いています。
具体的にはファンデルワールス力、双極子-双極子相互作用、クーロン力などです。
これらは共有結合やイオン結合などの化学結合に比べて非常に弱い力ではありますが、どれか一つというわけではなく、様々な種類の力が複合的に作用しているため、これらをすべて考慮するとなると非常に議論が複雑になってしまいます。
そのためこれらの分子間力も理想気体では生じないものとして考えます。

③高圧・低温の条件でも気体状態のままであるとする

実際には気体の温度をどんどん下げていくと分子の運動は弱まっていき、やがて気体から液体、固体へと変化します（分子の種類と圧力の条件によっては液体を経ずに気体からいきなり固体になることもあります）。

また圧力をどんどん上げていくと気体分子は周囲から押さえつけられる力が強くなり、運動が弱まって、同様に液体や固体になります。

ボイル・シャルルの法則などはあくまでも気体を想定したものなので、液体や固体になると議論ができなくなってしまいます。
そのため、たとえ絶対零度まで温度を下げたり、非常に強い圧力をかけたりしても気体の状態であるものとして考えます。

理想気体に近づけるには

しかし、そうはいっても現実と理想には差があります。
その差を埋めてできるだけ理想気体に近い状態を作るにはどのような条件にすればよいかというと、次の2つの条件が考えられます。

　①高温にする
　②低圧にする

高温にすることで分子はエネルギーを得て運動が活発になり、気体状態のままでいられます。
また高速で動き回っている状態では他の分子と接触する時間が短くなるため、分子間の相互作用は起こりにくくなります。

低圧にすると分子同士の距離が広がるため、このことによっても分子間の相互作用が起こりにくくなります。
また気体全体の体積が大きくなると分子自体の体積が占める割合は小さくなるため、分子自体の体積の影響を受けにくくなります。

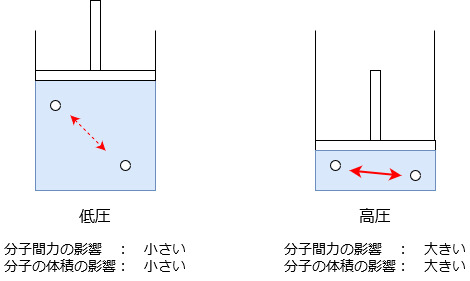
理想気体からのずれ

では実際に気体分子がどれくらい理想気体からずれているのか、グラフを見てみましょう。

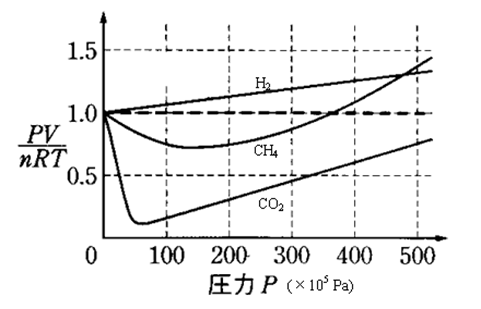
横軸は圧力Pです。

縦軸は気体の状態方程式　PV=nRT　を変形したものですが、
ここでRは気体定数という定数なので一定であり、温度Tも一定、気体の物質量nも一定です。
理想気体では上記の状態方程式が成り立つはずですので、圧力の変化によらずPVが一定の値となるはずです。
上のグラフでは破線で示されているものが理想気体になります。

しかし、他の気体（水素、メタン、二酸化炭素）を見ると理想気体からのずれが生じていることがわかります。
そしてそのずれ方には、理想気体より上側にずれているのか下側にずれているのか、という違いがあります。

理由はこうです。

理想気体よりも上側にずれる場合：分子自体の体積の影響を受けている
理想気体よりも下側にずれる場合：分子間力の影響を受けている

先ほど理想気体に近づけるには圧力が低い方がよいという理由を書きましたが、圧力を高くした場合にはその逆の現象が起きると考えられます。
つまり、圧力が高いと分子同士の距離が縮まって分子間の相互作用の影響が大きく出るようになり、また気体全体の体積に対する分子自体の体積の影響が大きくなります。

グラフを見ると気体の種類によってどちらの影響が出やすいかが変わることが見て取れます。
これはもともと分子間力が強い物質は分子間力の影響が強く出やすいためです。

どのような物質なら分子間力が強いのかというと、分子の極性（分子の中のプラスとマイナスの電荷の偏り）が強いものになります。
なぜ分子が極性をもつのかというと、分子を構成する原子の電気陰性度に差があるためです。
電気陰性度とは、原子が他の原子から電子をひっぱってくる力の強さを表したものです。
電気陰性度の大きい原子は他の原子から電子をひっぱるのでややマイナスに偏り、電気陰性度の小さい原子はもっている電子を他の原子にひっぱられてややプラスに偏ります。

先ほどのグラフに示された３種類の気体について分子の極性を確認するために、
ポーリングの電気陰性度を使って比較してみます。

水素に関しては、H同士の電気陰性度は同じですから電気陰性度の差は0で無極性となります。
グラフを見ても理想気体より下側にずれてはいないことがわかります。

メタンの場合はC-H間の電気陰性度の差が2.5-2.2＝0.3となります。

二酸化炭素はO-C間の電気陰性度の差が3.5-2.5＝1.0となります。
電気陰性度の大きな酸素が含まれているため、メタン分子の極性よりも二酸化炭素の極性の方がずっと大きくなります。
グラフを見ても二酸化炭素の方が下側へずれる幅が大きいことがわかります。
（数値はこちらより引用）

特許明細書の中での理想気体

理想気体について見てきたので、特許明細書の中でどのように理想気体という言葉が使われているのか確認しました。
分野としては圧力センサー、タイヤ、ロケットエンジンなどで、ほとんどが「理想気体の状態方程式」という言葉で出てきました。
気体の状態方程式を使うと、ある一定の温度条件下で決まった体積の容器にガスが入っていればその容器にかかる圧力は一定になるはずなので、そうならない場合にガス漏れを検出できる、ということは講座ビデオでも説明がありました。

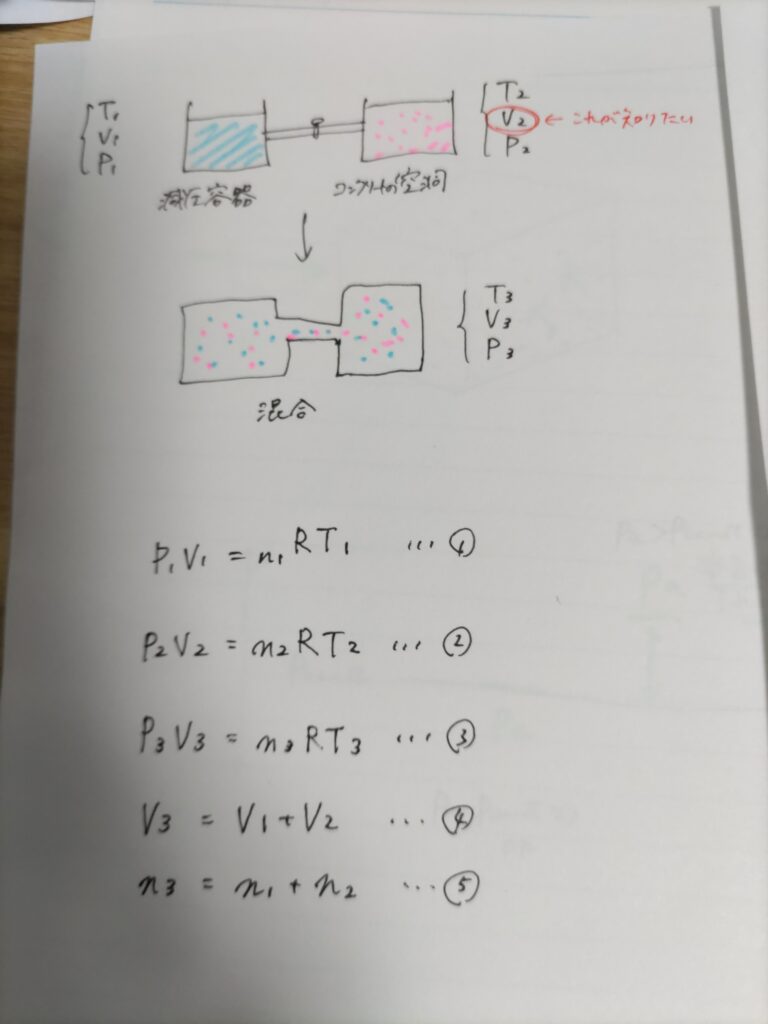
その他少々変形したものとしては、気体の状態方程式からコンクリートの空洞を算出する、というものがありました。
まず容積のわかっている減圧容器を用意し、容積のわからないコンクリートの空洞部分と開閉バルブで連結します。
そして開閉バルブを開けてこの2つの気体を混合します。
このとき減圧容器の気体の圧力と温度、空洞部分の気体の圧力と温度、混合気体の圧力と温度を計測しておけば、
３種類の気体それぞれについて状態方程式を考えて、コンクリートの空洞部分の体積を算出できるようになる、というものです。

明細書に丁寧に求め方が書いてあったので検算してみました。
岡野の化学でやったドルトンの分圧の計算問題とよく似ています。

また、理想気体と実際とは違いますよ、ということについてもただし書きがありました。
低圧条件にすれば理想気体に近づける、という話がそのまま出てきていました。

「圧力等の計測対象となる気体には、空気を用いる。勿論、空気は、窒素、酸素、水蒸気、二酸化炭素、その他微量気体からなる実在混合気体であり、理想気体ではない。理想気体の状態方程式は、分子自身の大きさと分子間力の影響を無視しているため、理想気体の状態方程式を実在気体に適用すると高圧条件になるほど誤差が大きくなってしまう。しかし、理想気体ではなく実在気体であっても低圧条件では理想気体に近い挙動を示すため、本発明のコンクリート構造物の空洞量推定方法では、計測対象気体である空気を減圧環境で計測することで誤差なく理想気体の状態方程式を適用できるようにしている。」

その特許技術の性能や有効性を理論にあてはめて証明するために、現実とは違うけれども理想気体というものを考え方るのですね。

7/10（水）学習時間：9H
・岡野の化学（158）
・理想気体について特許を参照
・自由体積について特許を参照
課題）
・自由体積と誘電率の関係について

その他
・4438　インプットとアウトプットの関係
・Just Right Proを購入したのでブログ記事の校正に使ってみたところ、自分では見落としていた変換ミスや回りくどい表現を指摘してくれた。
他にも色々機能がありそうだが調べ切れていないので少しずつ使いこなせるようにしたい。
・睡眠時間を削りすぎてしまったので今日は早めに寝る。