今回の記事では、毛細管現象の物理的原理と、前回に引き続きBio-Rad社のddPCR特許における応用例を取り上げ、表面張力・濡れ・接触角・分子間力との関係を体系的に解説します。
毛細管現象は、植物が根から水を吸い上げる仕組みや、タオルが水を吸収する現象など、私たちの身の回りで広く見られる物理現象です。表面張力や濡れ性、接触角といった現象がどのように関係しているのかを知ることは、材料開発やマイクロ流体デバイスの設計にもつながる重要なテーマです。
今回は、毛細管現象がなぜ起こるのかを、図解をまじえて分子の挙動として直感的に捉えつつ、毛管上昇高さの公式など、関係する数式の意味を丁寧に説明しました。
最後に、Bio-Rad社特許(WO2014205447A2)の該当部分を自力翻訳し、技術内容を翻訳の観点からも考察します。
目次
毛細管現象とは
毛細管現象とは、細い管(毛細管、毛管)に液体を接触させたときに、外部からの明示的な圧力を加えなくても、液体が管内を自発的に上昇・下降する現象です。
これは、後述するように、液体の表面張力と管との濡れ性、重力とのバランスによって生じます。
液体の表面張力、管表面への付着力、重力のバランスが取れるところまで液面は上昇します。
毛細管の場合は管の直径が小さく、同じ高さでも直径が大きい場合の管よりも上昇した水の重さが軽くなるため、液体が比較的高く上昇します。したがってこのような現象は毛細管に顕著にみられます。
身近な毛細管現象
毛細管現象は、日常の様々なところで観察できます。
例えば、以下のようなものがあります。
- 植物の根が水分を吸い上げる
- 毛髪に水分が行きわたる
- タオルに水が染み込む
- ガラスペンにインクをつける
- フレンチトーストを作るときにパンに卵液を染み込ませる
- 屋根材同士の間の細い隙間から雨漏りする
分子間にはたらく力
分子間力とは、その名の通り、分子と分子の間にはたらく力です。
原子と原子の間にはたらく力は、共有結合、イオン結合、金属結合など、原子間の電子の受け渡しや共有を伴う化学結合ですが、分子間力はそのような電子のやり取りを伴わない物理的相互作用であり、より弱い結合です。
ここでは、代表的な分子間力である、
- ファンデルワールス力
- 双極子−双極子相互作用
- 水素結合
について紹介します。
ファンデルワールス力
まず、電子は教科書でよく見る電子配置のようにきれいに並んでいるわけではなく、あるときはこちら、あるときはあちら、というように常に移動しています。
そのような電子の存在を確率論的に表すと、下図のような電子雲のモデルになります。
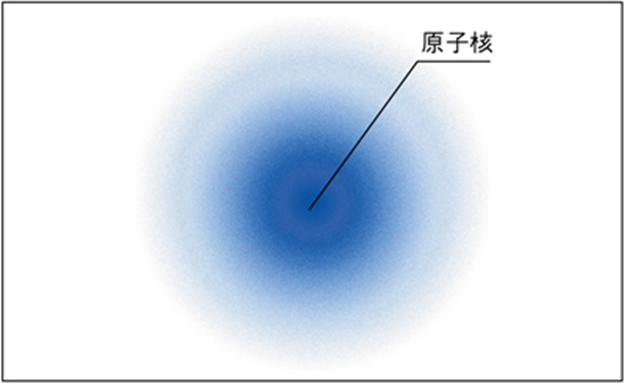
したがって、水素分子(H2)のような非極性分子と呼ばれるものでも、ある一瞬を切り取れば電子の偏りが生じていて一時的に極性を持つことがあります。
そのような一時的な電子の偏りによって分子同士が引き付けあったり、逆に反発しあったりする相互作用のことをファンデルワールス力と呼んでいます。
双極子-双極子相互作用
双極子-双極子相互作用とは、すでに極性を持っている分子同士が、その極性の偏りによって生じる静電気力で引き合ったり反発しあったりする相互作用です。
ここで、電気陰性度というものを考えます。
電気陰性度とは、共有結合において、各原子が電子対を引き付ける力の強さを表しています。
17族のハロゲン原子は、あと1個電子が入れば最外殻が電子で満たされて希ガスと同じ安定な電子配置になるため、電気陰性度が高くなっています。
反対に、1族の原子は自分の持っている電子を1つ手放すことで希ガスと同じ安定な電子配置になるため、電子をもらいたがらない、つまり電気陰性度が低くなります。
さらに、原子の大きさが小さいほど、原子核と最外殻との距離が近くなるため、核が電子を引き付ける力が強く、電気陰性度が高くなります。
希ガスを除き上記の一般的傾向を周期表で表すと、周期表の右に行くほど、さらに同じ族であれば上に行くほど、下図のように電気陰性度が高くなります。
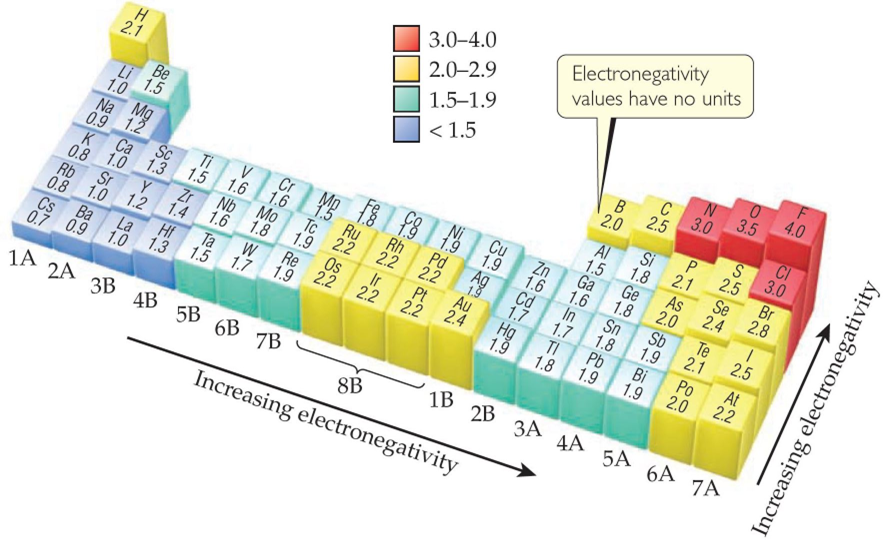
(画像引用元:https://chemistry.com.pk/general-chemistry/electronegativity-chart-pdf/attachment/electronegativity-trends/)
したがって、共有結合の中でも、電気陰性度の違いによってわずかな電子の偏り(分極)が生じています。このような分子を双極性分子と呼びます。
ただし、双極性分子、非双極性分子、イオン結合分子の間に明確な線引きがあるわけではなく、分極の程度によって便宜上分けられています。
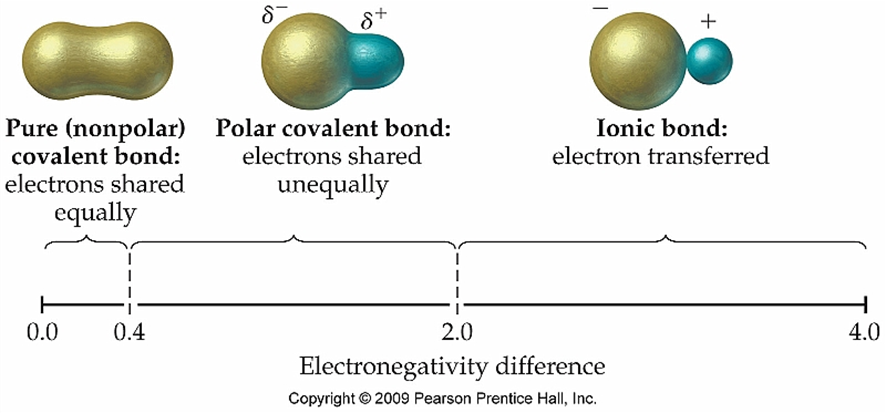
(画像引用元:https://kaiserscience.wordpress.com/chemistry/bonding/polar-bonds-and-molecules/)
水素結合
水素結合は、分子間力の中でも特殊な、比較的強い結合です。
水分子はご存じの通り、水素原子と酸素原子によって構成されています。
水分子の構成では、先ほどのポーリングの電気陰性度を見ても分かるように酸素原子が水素原子との共有結合電子を強く引き付けるため、下図のようなわずかな分極が生じています。
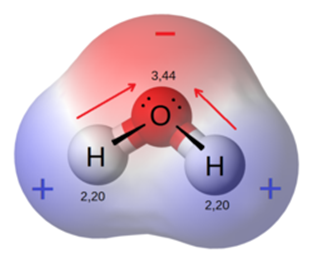
この分極がさらに別の分子を引き付けるため、水分子は下図のように分子同士が比較的強く結合する水素結合を作ります。
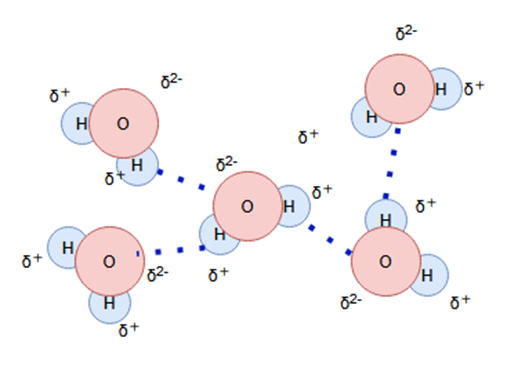
このように、電気陰性度が高い原子(フッ素・酸素・窒素原子)に共有結合で結びついた水素原子が、その近傍にいる別の分子中の電気陰性度が高い原子との間につくる結合のことを水素結合といいます。
表面張力とは
さて、液体内部では液体分子同士に上述のような分子間力が働いて凝集していますが、表面ではどうなるでしょうか?
液体内部と液体表面での分子間力を非常に簡略化すると、下図のようになります。
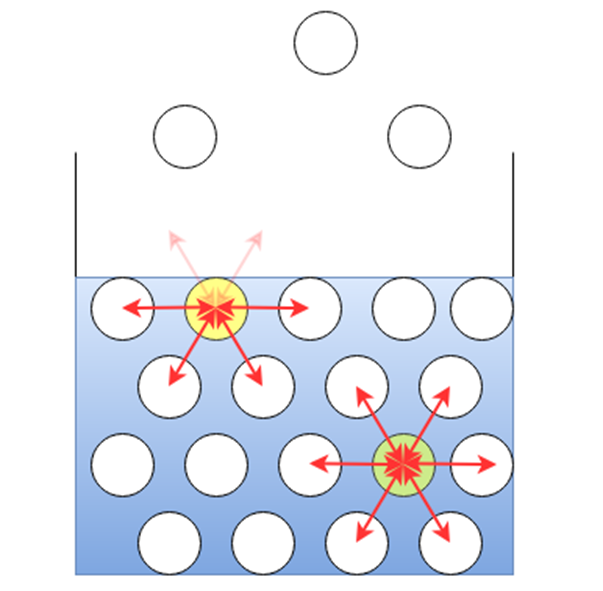
このとき、液体内部の分子は周囲の分子から等しい力を受けて安定していますが、表面の分子は上部に液体分子がいないため(もちろん気体分子はいますが、液体分子と比べて数が少ないため、相互作用が非常に小さい)、大気側に引き合う相手を求めて余分なエネルギーが存在する状態になっています。
この状態は不安定であるため、液体は表面に触れる面積が最小になるようにまとまろうとします。
このように、液体が表面に触れる面積を最小にしようとする力が表面張力です。
表面張力の定義―マクスウェルの枠
表面張力の定義にはいくつかの説明がありますが、有名でわかりやすいものとして「マクスウェルの枠」による定義を説明します。
まず、コの字型の枠があり、そこに可動棒がはまっていると仮定します。
この枠と可動棒で作られる面積には液体の膜が張っていると考えます。
先ほど、表面張力について、表面を最小にするようにはたらく力という説明をしましたが、可動棒をひっぱろうとすると、それに抵抗するように、表面に平行に膜を収縮させる向きに、可動棒に対して力がはたらくことになります。単位長さあたりのこの収縮力が表面張力です。
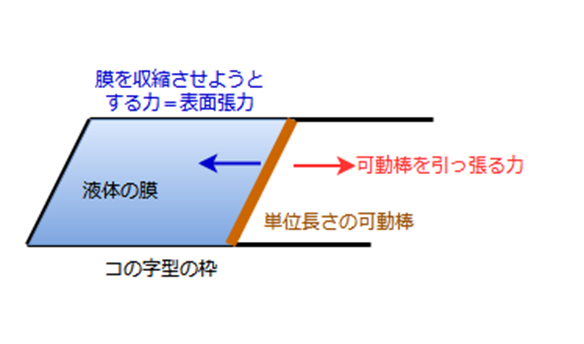
言い換えれば、表面張力は、単位長さの線を引っ張るのに必要な力ということにもなります。
力の単位はN(ニュートン:1kgの質量を持つ物体に1m/s2の加速度を生じさせる力)で定義されますので、したがって、表面張力はmN/m(ミリニュートン毎メートル)という単位であらわされます。
N/mではなくmN/mが使用されているのは、mN/mにすると、CGS単位系(長さの単位にセンチメートル、重さの単位にグラム、時間の単位に秒を用いる単位系)で使用される表面張力の単位dyn/cmと数値がイコールになるためだと思われます。
表面張力と表面自由エネルギー
表面張力と似た概念で、表面自由エネルギーというものがあります。
表面張力(mN/m)は、先ほど説明した通り単位長さの線を引っ張るのに必要な力ですが、表面自由エネルギー(mJ/m2)は、単位面積の面を広げるのに必要なエネルギーと表現されます。
単位面積あたりなので、表面張力の単位(mN/m)の分母にmをかけてm2を作ります。
分母をm倍したら分子もm倍しないといけないので、分子はmN×mになります。
ここで、J(ジュール)は、1Nの力がその力の方向に物体を1メートル動かすときの仕事量として定義されますので、mN×m=mJと置き換えられます。
したがって、表面張力(mN/m)と表面自由エネルギー(mJ/m2)は、概念と単位は異なりますが、同じ次元として扱うことができます。
では、どういうときに表面自由エネルギーを使うのでしょうか。
表面張力は先ほど説明したように、液体が表面積を縮めようとする力でした。液体分子は比較的自由に動くことができるため、表面を縮めるという考えがなりたちますが、固体の場合には分子はほぼ静止しているため、そのような考えが成り立ちません。
具体的に水の状態変化を考えてみれば、水蒸気(気体)⇒水(液体)⇒氷(固体)と変化するにつれて分子の運動が小さくなっていくことがイメージできるかと思います。
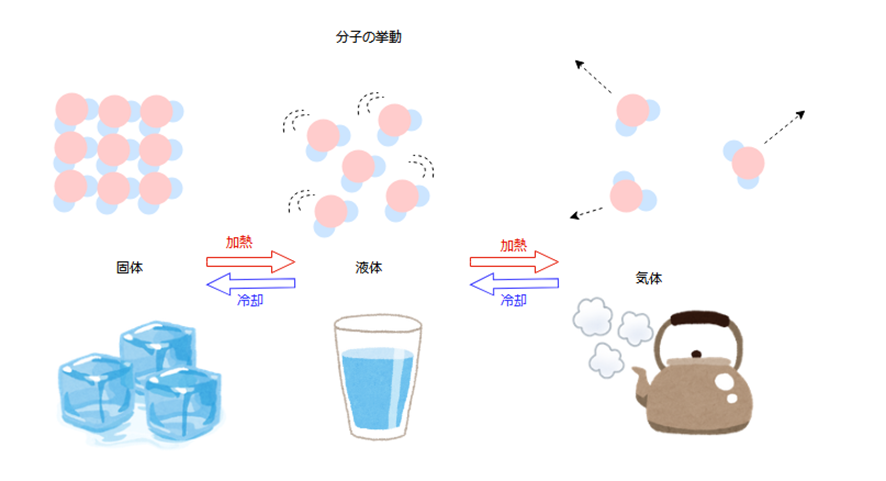
しかし、固体の場合も表面部分では分子が引き合う相手を持たず、液体の場合と同様に余分なエネルギーが生じています。これを表面自由エネルギーと呼んでいます。
そもそも、表面張力と表面自由エネルギーには、「力」と「エネルギー」という違いがあります。
力とは、物体を変形させたり、物体の運動状態を変化させたりするものとして定義されます。これは、速度や加速度と同じく、向きをもったベクトル量です。
エネルギーは、仕事(ある物体をある方向に移動させること)をする能力です。これは、温度や時間などと同じく、向きを持たないスカラー量です。
表面自由エネルギーは、潜在的に表面を収縮させる能力をもっているというだけで実際に表面を収縮させるわけではないので、分子が静止状態にある固体表面についても当てはめられる概念です。
したがって、表面自由エネルギーは、液体か固体かを問わず、あらゆる表面が持っているエネルギーといえます。
そこで後述する濡れ性に関して、固体の濡れ性を考える際などは、表面自由エネルギーが用いられます。
濡れ
表面張力についてみてきたところで、今度は表面張力と非常に関係の深い「濡れ」についてみていきましょう。
濡れとは
濡れ性とは、分かりやすく言えば液体と固体のなじみやすさのことです。
例えば、水滴を紙の上に落とすとベタっと広がっていきますが、葉っぱの上でははじかれて丸くなります。

(画像引用元:https://kids.gakken.co.jp/jiyuu/category/try/water_repellency_of_leaves/)
あるいは同じところに垂らすのでも、一般的には油の方が水よりもベタっと広がりやすくなります。
もう少し正確に「濡れ」を定義すると、「固体と気体の界面(固体表面)が、液体によって置換されて、新たに固体-液体界面が形成される現象」ということになります。
固体表面の空気に触れていた部分に液滴が濡れ広がってくれば、その部分が液体で置き換わるということです。
液体の表面張力が大きければ液体は丸くなりますが、固体表面となじみやすければその丸みは小さくなります。
濡れの種類
濡れには、
- 付着濡れ
- 浸漬濡れ
- 拡張濡れ
- 浸透濡れ
の4種類があります。
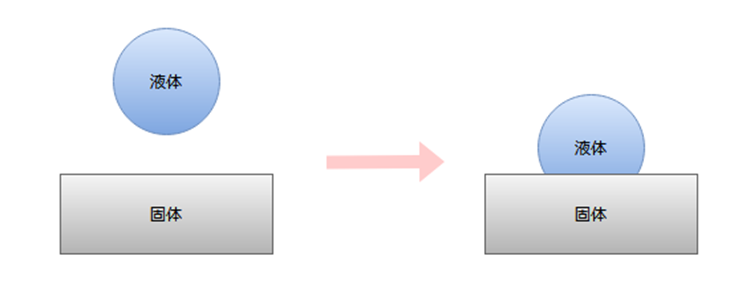
付着濡れ
最も基本的な濡れであり、気相中の固体表面に液体が液滴として付着する濡れです。
塗装、コーティング、接着、親疎水性表面の評価などに関係します。
次項で解説する接触角θについては、0°<θ<180°の値を取ります。
浸漬濡れ
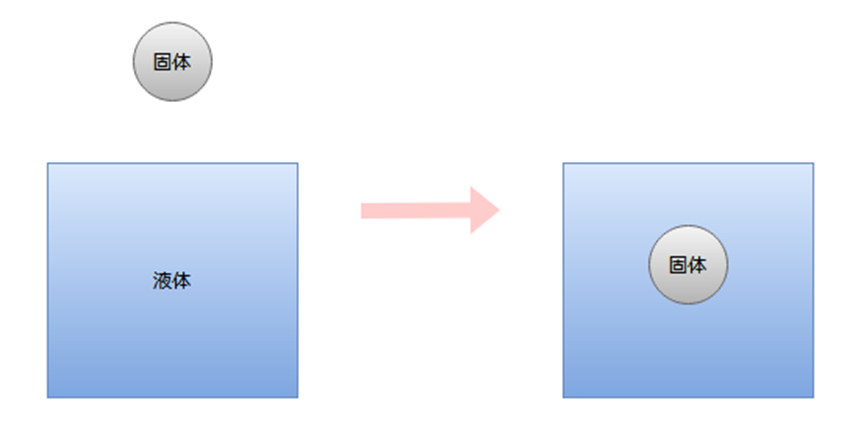
固体が液体中に没し,表面全体が液体におおわれるような濡れです。
粉体を液体中に分散させることは、この「浸漬濡れ」に相当します。
接触角θについては、0°<θ≦90°の値を取ります。
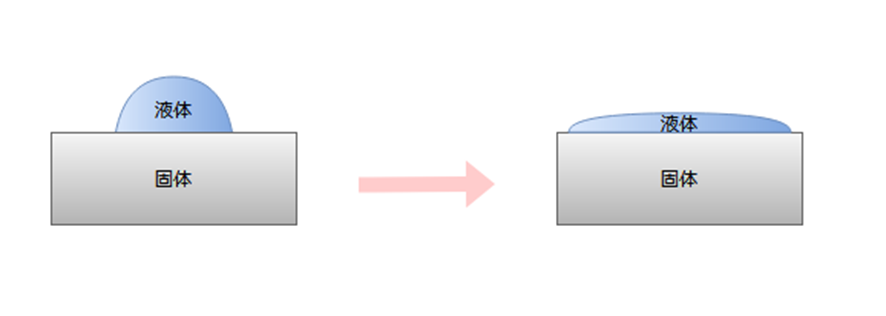
拡張濡れ
液体が固体表面を濡れ広がっていくような濡れです。
インクジェット印刷、農薬の葉面散布などに関係します。
接触角θは、ほとんど0°の状態です。
浸透濡れ
液体が微細な孔や毛細管など内部に浸み込んでいく濡れです。
今回のテーマである毛細管現象は拡張濡れにあたります。

接触角
濡れ性は、接触角を用いて表すことができます。
液滴の接線と固体表面とのなす角度θを接触角と定めます。
接触角と濡れやすさ
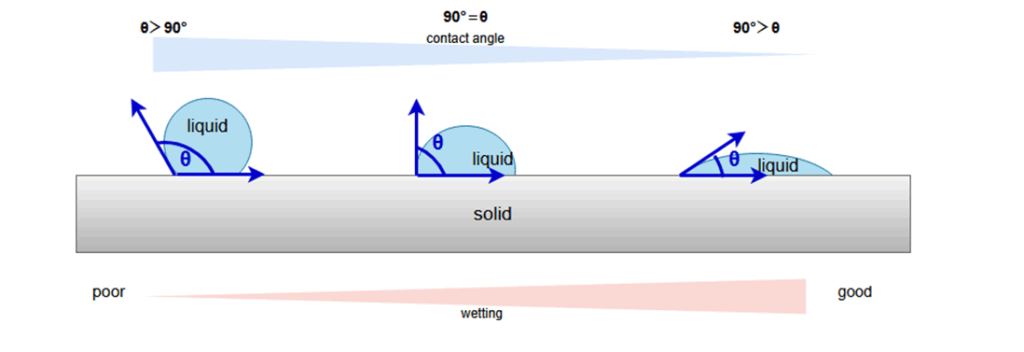
図をみると分かるように、接触角が大きくなるほど濡れにくく、接触角が小さくなるほど濡れやすいといえます。
接触角θが90°≦θ≦180°の時には濡れない、0°≦θ<90°のときには濡れると評価します。
液滴を水として表面の性質に注目した場合には、
接触角θが90°≦θ≦180°の時に撥水性表面、0°≦θ<90°のときに親水性表面となります。
接触角の測定方法
では、続いて接触角をどのように測定するのかをみていきましょう。
デジタルカメラと画像解析
接触角は、カメラと画像解析装置を用いて測定することができます。
PC普及以前にはカメラのファインダーを覗いて分度器を用いて目視で測定していましたが、現在はデジタルでの画像解析できるようになっています。
下の写真のような装置を用い、バックライトで液滴に光を当て、その反対側からカメラで液滴の画像を捉えます。
捉えた画像の液滴にカーブを重ね合わせて端点での微分係数を求めることで、容易に接触角を求めることができます。

θ/2法
上記のような微分係数の計算ができない場合に、比較的簡単に接触角を求められるのがθ/2法という方法です。
この方法は、液滴を球の一部に近似して角度を計算するものです。
まず、液滴の画像から端点から端点までを二等分して点Dを取ります。
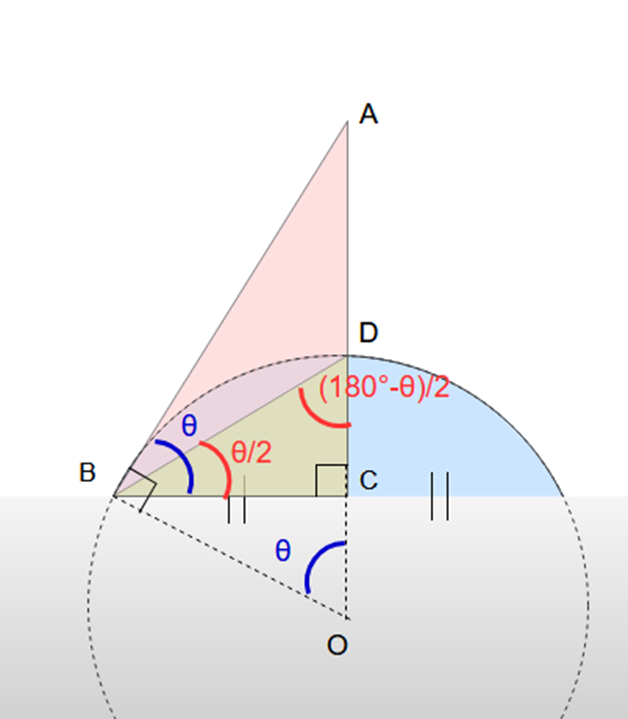
液面が球の一部である場合、接触角∠ABCをθとすると、△ABOと△ABCの相似から∠AOB=θとなります。
また、円の半径から、辺OB=辺ODとなるため、△OBDは二等辺三角形となります。よって∠OBD=(180°-θ)/2となります。
ここで、△CBDの内角の和の関係から、∠DBC=θ/2ということが求められます。
あとは、この∠DBCを測定して、そこから∠DBC=θ/2により接触角θを導き出すことができます。
接触角測定の注意点 その1―動的・静的接触角
接触角測定において注意しなければならないことのひとつに、動的か静的か、という問題があります。
固体表面に滴下した液体は、すぐに濡れ広がるとは限らず、時間をかけて徐々に濡れ広がって一定の角度に落ち着く場合があります。
そのため、静的接触角の場合は、滴下してから測定までにかかる時間にも注意して測定を行う必要があります。
あるいは、動的接触角を測定するという方法もあります。
以下に動的接触角の測定方法として、拡張収縮法と滑落法を紹介します。
動的接触角測定法①―拡張収縮法
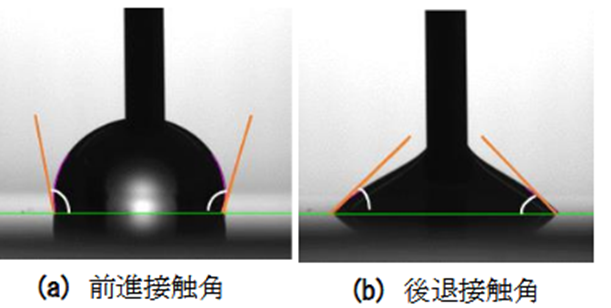
拡張収縮法は、平らな固体表面に載せた液滴に、垂直に立てた針先から液体を一定時間吐出(拡張)、吸引(収縮)し、液滴との接点が拡張、あるいは縮小し始めたときの接触角を測定する方法です。
拡張開始時の接触角を前進接触角、縮小開始時の接触角を後退接触角とし、その差によって濡れ性を評価します。
動的接触角測定法②―滑落法
滑落法では、下図のように固体の斜面に液滴を垂らし、その液滴がすべり落ちる寸前の状態において、前進接触角と後退接触角を測定します。
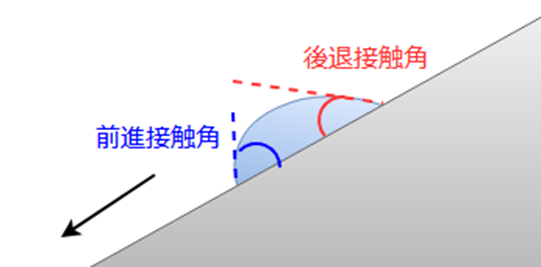
このとき、測定した前進接触角から後退接触角を引いた差は接触角ヒステリシス(接触角履歴)と呼ばれ、この値が小さいほど液滴は形を変えずに容易に転がっていくということになり、液滴の除去性が高い表面と判断することができます。
これは、例えばお風呂の壁、シンク、トイレの表面など、汚れが勝手にするっと落ちてくれる自己洗浄性が求められる表面材料の評価に役立ちます。
接触角測定の注意点 その2―表面粗さ
もう一点、接触角の測定時に注意しなければいけないのは、固体表面の粗さです。
固体表面はいつも滑らかであるとは限りません。
例えば、凹凸のある表面では、下図のように実際の接触角θroughと、凹凸を補正した見かけの接触角θsmoothには差があることがわかります。
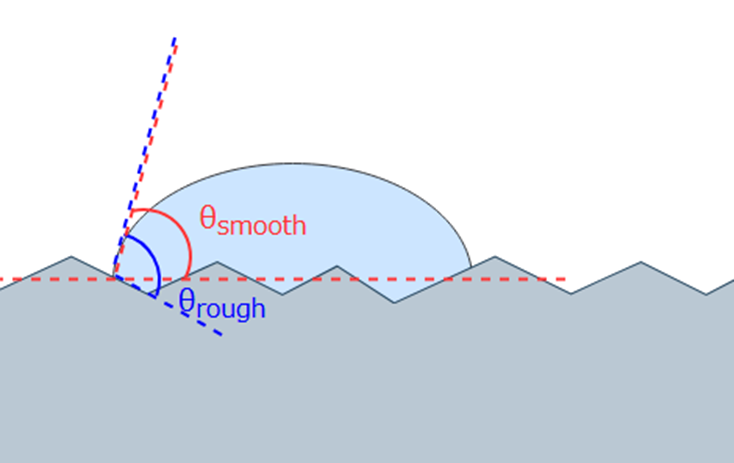
このとき、両者の接触角の間には、Wenzelの式と呼ばれる以下の関係式が成り立ちます。
Wenzelの式:
ここでのrは、表面粗さ係数であり、実際の表面積を見かけの面積で割った値です。
r=1であれば完全に平坦であり、そこからrの値が大きくなるほど、表面が粗くなっていきます。
ここで、表面粗さがある場合にr>1であることとWenzelの式から、以下の関係が成り立ちます。
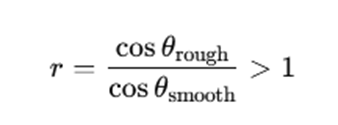
では、次にθがどのような値をとるときに上記の関係が成り立つのかを考えてみましょう。
下のグラフの青い曲線は、θの変化に応じたcosθの値の変化です。
赤い縦線で示したπ/2(=90°)のところでcosθの値の正負が入れ替わるというのがポイントです。
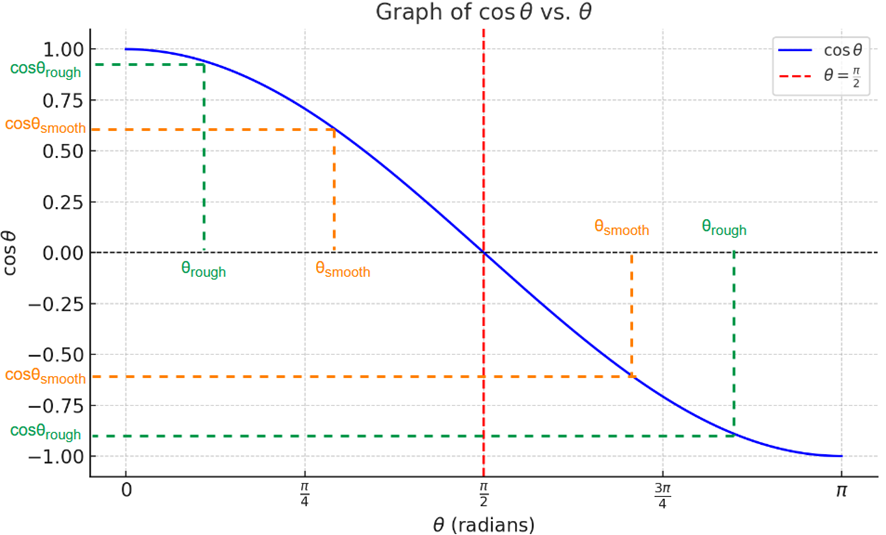
また、接触角θは小さいほど濡れやすく、大きいほど濡れにくいので、θの値によって表面粗さと濡れやすさの条件は以下のように整理できます。
- θ<π/2の範囲では、θrough<θsmooth
すなわち、粗い表面の濡れやすさ > 滑らかな表面の濡れやすさ - θ>π/2の範囲では、θrough>θsmooth
すなわち、粗い表面の濡れやすさ < 滑らかな表面の濡れやすさ
また、先に説明した通り、θ<π/2は濡れている、θ>π/2は濡れていない状態ですので、上記条件にさらに当てはめて図として整理すると以下のようになります。
- θ<π/2 :濡れている表面では、表面が粗いほどより濡れやすい
- θ>π/2 :濡れていない表面では、表面が粗いほど濡れにくい
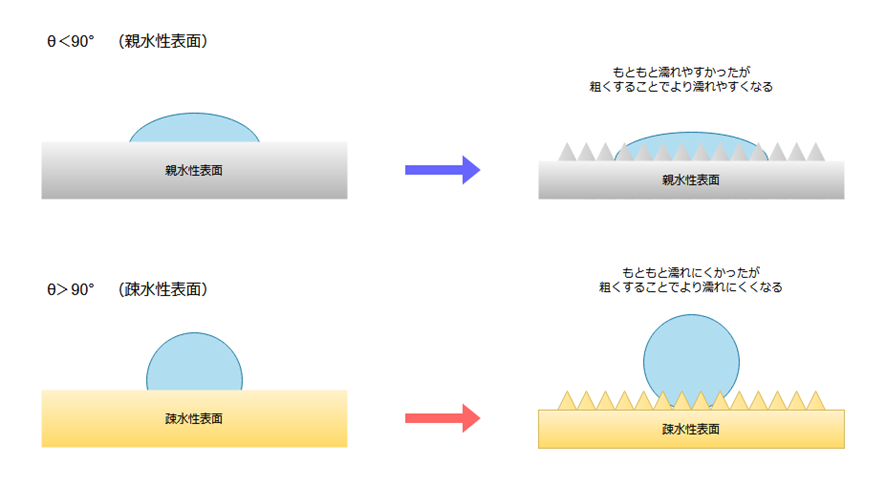
したがって、壁に塗装をする際に、壁面に塗液をしっかり付着させたい場合には、上図の上部のように、壁面を親水性に加工したうえでさらに表面を粗くするのが効果的ということになります。
図の下部は、ハスの葉の撥水性から発見されたロータス効果としても有名です。
例えば、ヨーグルトの蓋に中身がくっつかないようにしたいときには、蓋の表面を疎水性にし、かつ凹凸をつけておけば、より効果的というわけです。
濡れ性と表面張力と接触角の関係
表面張力が大きければ液滴は丸くなりやすくなるため、接触角は小さくなります。
したがって、一般的に、接触角が大きいほど表面張力は大きく、接触角が小さいほど表面張力は小さいということになります。
ただし、先ほど述べたように、濡れは液体自体の表面張力だけでなく、固体表面の影響も受けます。
このような固体表面に液体が接触したときの濡れを、液体の表面張力、固体の表面自由エネルギー、固体と液体の間の界面張力、および接触角との関係で表したYoungの式というものがあります。
Youngの式
Youngの式は、固体表面に液体が接触したときの濡れを、液体の表面張力、固体の表面自由エネルギー、固体と液体の間の界面張力、および接触角との関係で表したものです。
表面張力と表面自由エネルギーとが一緒の式になっていますが、先ほど説明したとおり、両者は同じ次元で扱うことができるため、等式で結ぶことができます。
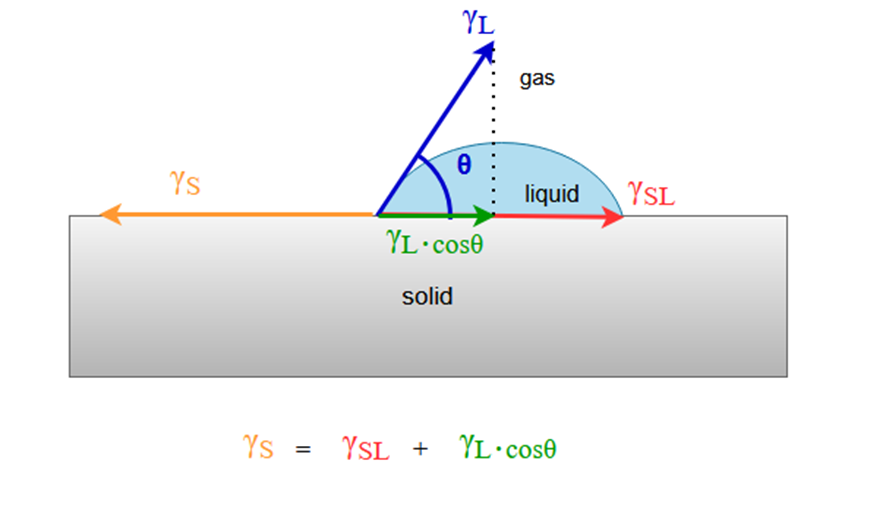
Youngの式:
γS :固体の表面自由エネルギー
γSL :固体-液体界面の自由エネルギー
γL :液体の表面張力
θ : 接触角
図にすると次のようになります。
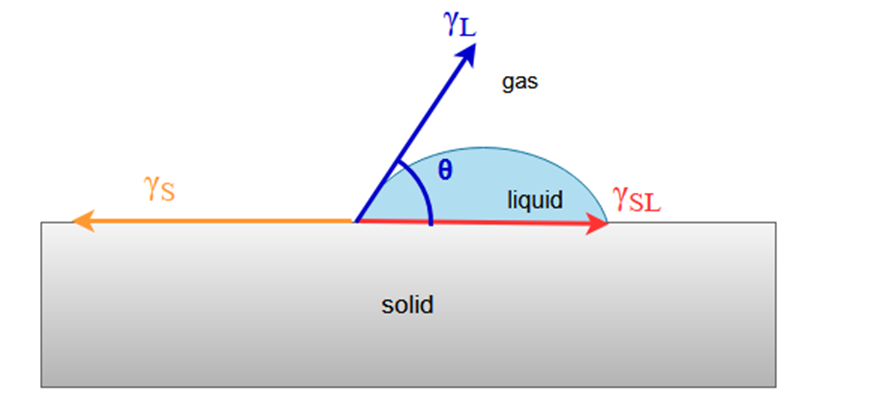
ここで水平方向の成分だけに注目して力のつり合いを考えれば、Youngの式が導かれます。
Youngの式から固体の表面自由エネルギーを求める
Youngの式は、固体の表面自由エネルギーを求めるのに役立ちます。
固体の表面自由エネルギー:γSを知りたい場合、γLは通常、文献から既に明らかであり、接触角θも上述のようにカメラを使った画像解析で測定することができるため、あとはγSLの値がわかれば、Youngの式に当てはめて固体の表面自由エネルギーを求めることができます。
ここで、γSLの値を求めるために、自由エネルギー変化量⊿Gというものを考えます。
これは、系全体のエネルギーが反応の前後でどのくらい変わるかを示したものです。
系全体のエネルギーは、ギブズ自由エネルギーと呼ばれる、エンタルピー(系がもつ熱的エネルギー)とエントロピー(系が持つ乱雑さ)のバランスをとった指標で表されます。
ギブズ自由エネルギーGは、次の式で表されます。
G=H-TS
(G:ギブズ自由エネルギー、H:エンタルピー、T:温度(ケルビン)、S:エントロピー)
そして、Gが大きいほどエネルギーの高い不安定な状態、Gが小さいほどエネルギーの小さい安定な状態であるため、系全体のGが小さくなる方向に、自発的な変化が生じます。
自由エネルギー変化量⊿G=G変化後−G変化前についていえば、ある事象が自発的に起きているのであれば、⊿G<0になっているということです。
例え話として、子供のお片付けでイメージしてしましょう。
子供が片づけをする意欲をGとして、各成分を以下のように考えます。
H:片づけるのにかかる労力
S:散らかっている方が自由に遊べるという自由度の高さ
T:楽をしたい気持ちの強さ(Sにどれだけ価値を感じるか)
ここで、お母さんが見ているときをG変化前としましょう。
このとき子供はきちんと部屋を片付けています。
・楽をしたい気持ち(T)は小さく抑えられている(監視下)
・散らかっていないので自由度(S)は低い
・でも頑張って片づけているから労力(H)は大きい
よって、G=H-TSは全体として高くなります。
次に、お母さんが出かけたときをG変化後としましょう。
このとき子供は部屋を散らかしています。
・T(楽をしたい気持ち)が上昇
・S(自由度)も上がる
・H(労力)は小さい(ほとんど片づけてない)
よって、G=H-TSは全体として低くなります。
この例えでは、Gが高い方(無理して片付ける状態)からGが低い方(自由で楽な状態)へ向かって自然な変化が起きています。つまり、子供が「お母さんが見てないときに部屋を散らかす」のは、ギブズ自由エネルギーが小さくなる自然な方向に進んだ結果ということになります。
さて、本題に戻って、付着濡れにおける系のエネルギー変化を考えてみます。
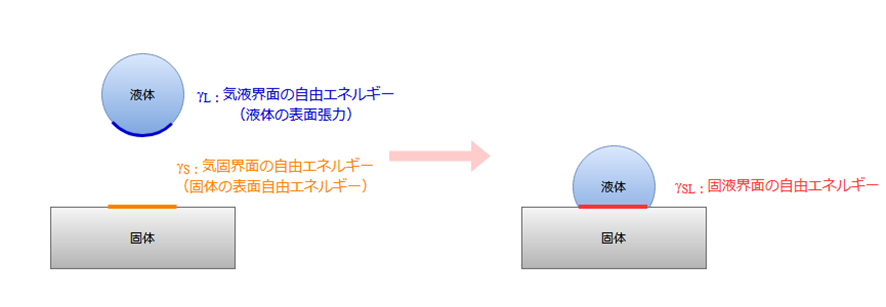
上図を参考に、付着濡れが起きる場合の付着部分のエネルギーを考えてみると、以下のようになっています。
濡れる前:G変化前=γL+γS
濡れた後:G変化後=γSL
そして、付着濡れは自発的に起こる現象であるため、自由エネルギー変化量⊿G<0となっています。
したがって、
⊿G=γSL-(γL+γS)< 0です。
よって、
γSL<(γL+γS)
となります。
では、γL+γSがγSLに変化した際に、逃げていったエネルギーは何なのでしょうか?
表面自由エネルギーは、相互作用する相手の分子がいないことで余剰になったエネルギーでした。ところが、液体分子と固体分子が接触することにより、相互作用の相手ができたのです。
したがって、余剰になっていたエネルギーの一部は、液体分子と固体分子の相互作用に変化し、あまったエネルギーがγSLとなったわけです。
この液体分子と固体分子の分子間にはたらくエネルギーをσSLとすると、固体側・液体側両方からの作用として係数2をつけて、次のように表せば等式が成り立ちます。
γSL+2σSL=γL+γS
冒頭で説明したように、分子間力にも色々な種類があるため、どの成分を考慮するかは様々な考え方がありますが、各分子間力は実験や理論計算による文献値として知られているため、それらの分子間力を平均したものを使います。
こうして2σSLが求められれば、先ほどの式、
γSL+2σSL=γL+γS
とYoungの式との連立方程式にして、
固体の表面自由エネルギーγSを求めることができます。
表面張力と界面活性剤の関係
液体の表面張力によって濡れ性は変化しますので、ある液体の濡れ性を変化させたいと思うとき、どのような方法がとれるか考えます。
その方法のひとつが界面活性剤の利用です。
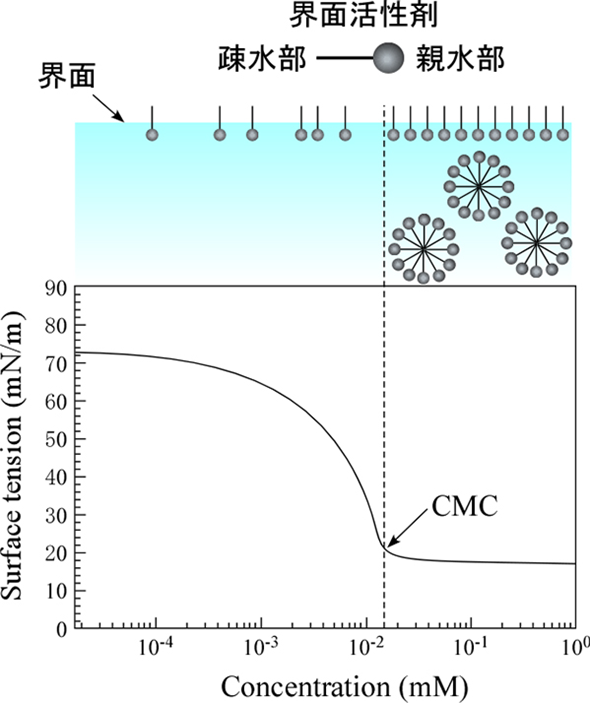
界面活性剤は、親水性部分と疎水性部分の両方を持つ特殊な物質です。
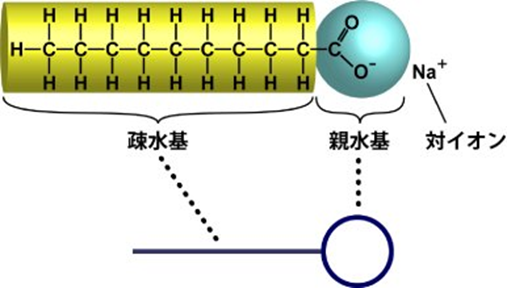
界面活性剤を水中に入れると、界面活性剤は液面に集まって、疎水基部分を上に向けて整列します。
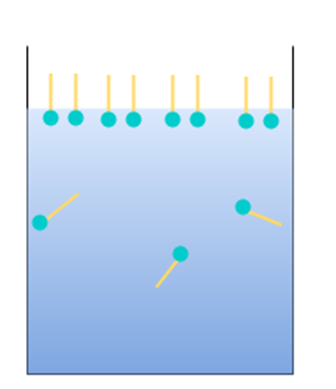
このように界面活性剤が液面に並ぶことで、液体分子同士の凝集力が抑えられるため、表面張力は低下します。
したがって、界面活性剤を用いることで、液体の濡れ性を高める効果が期待されます。
このとき、液面は界面活性剤の疎水基部分に置き換えられていくので、表面張力は油の値に近づいていきます。
また、界面活性剤をどんどん加えていくとあるところでそれ以上は液面に並べなくなり、代わりに界面活性剤同士が疎水基同士を内側に向けて集まり、ミセルと呼ばれる集合体を形成します。
このようにミセルを形成し始める界面活性剤の濃度は、臨界ミセル濃度(Critical Micelle Concentration; CMC)と呼ばれ、このときの表面張力は一定になります。
表面張力の測定方法
続いて、表面張力をどのように測定するのかを紹介します。
代表的なのは、
- ウィルヘルミプレート法
- デュ・ニュイリング法
- 滴重法
と呼ばれる3つの方法です。
ウィルヘルミプレート法
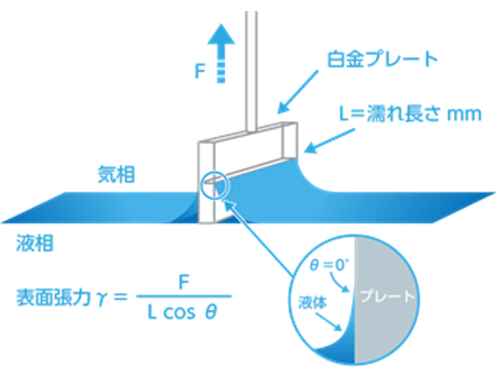
ウィルヘルミプレート法は、ウィルヘルミプレートと呼ばれる薄い白金プレートを液体に浸し、その際に液体がプレートを引っ張り込もうとする方向に発生する力を測定することにより、表面張力を計算する方法です。
(画像引用元:https://www.contact-angle.jp/contact-angle/surface-tension/measurement-principle/)

(画像引用元:https://www.is2m.uha.fr/en/technical-platforms/wettability/kruss-k14/)
この方法では、表面張力は下記の式で求めることができます。
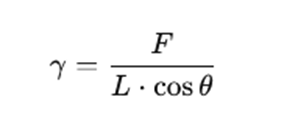
γ:表面張力(mN/m)
F :白金プレートにはたらく力(mN)
L :白金プレートの濡れ長さ(m)
θ:白金プレートと液体との接触角
表面張力の鉛直成分であるγ⋅cosθに濡れ長さLを掛けた力の大きさが、白金プレートを引っ張る力Fとつり合うため、F=γ⋅L⋅cosθがなりたち、これを整理すると上記の式になります。
デュ・ニュイリング法
デュ・ニュイリング法では、白金製のリング状の測定子を液面に接触させ、垂直に持ち上げていきます。すると、リングに液体の膜ができます。
先にマクスウェルの枠の話をしましたが、同様にこのリング平面にできた液体の膜にも、持ち上げる力に対抗して縮まろうとする力が働きます。
さらに測定子を持ち上げていくと、あるところで膜は耐え切れずに破けてしまいます。
膜が破ける寸前の力を表面張力として計算します。
滴重法(ペンダントドロップ法)
滴重法は、半径r(m)の毛管から液滴が落下する瞬間を考えます。
液滴は毛管の先端の周囲に沿って上向きに働く表面張力に支えられていますが、重力によって段々に成長していき、ついに表面張力でその重みを支えられなくなったときに落下します。
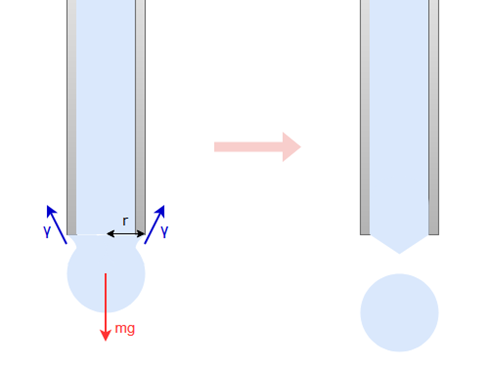
この落下寸前の液滴の質量をm(g)とすれば、この液滴に働く重力はmgと表されます。
また、この毛管に働く表面張力は、液体の表面張力γとすると、毛管の外周が2πrとなるため、2πrγとなります。
よって、下の関係式が成り立ち、表面張力γを求めることができます。
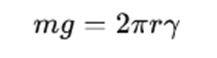
滴重法では、サンプルが少量で済み、また液滴が比較的ゆっくり落下する粘度の高い液体の測定に適しています。
ただし、実際には液滴落下時には一部が管の先端に残ったり、2つに分かれて落下したりと様々な現象が考えられるため、精度を高めるには補正が必要になります。
毛管上昇はなぜ起こるのか
ここまで、表面張力と濡れについての関係をみてきました。
最初の毛細管現象の話に戻りますが、なぜ毛管上昇が起きるのでしょうか。
毛管上昇で起きていること
ここで、毛管がガラス管である場合の構成について考えます。
ガラスの主成分は、二酸化ケイ素(SiO2)です。
二酸化ケイ素は、Siがsp3混成軌道という軌道を形成するため正四面体構造を取ります。
1分子だけではO原子が2個しかないので正四面体の4つの頂点のうち2つが余ってしまいますが、その頂点に他のSiO2分子のO原子が結合することで結合力の強い共有結合結晶を作ることができます。
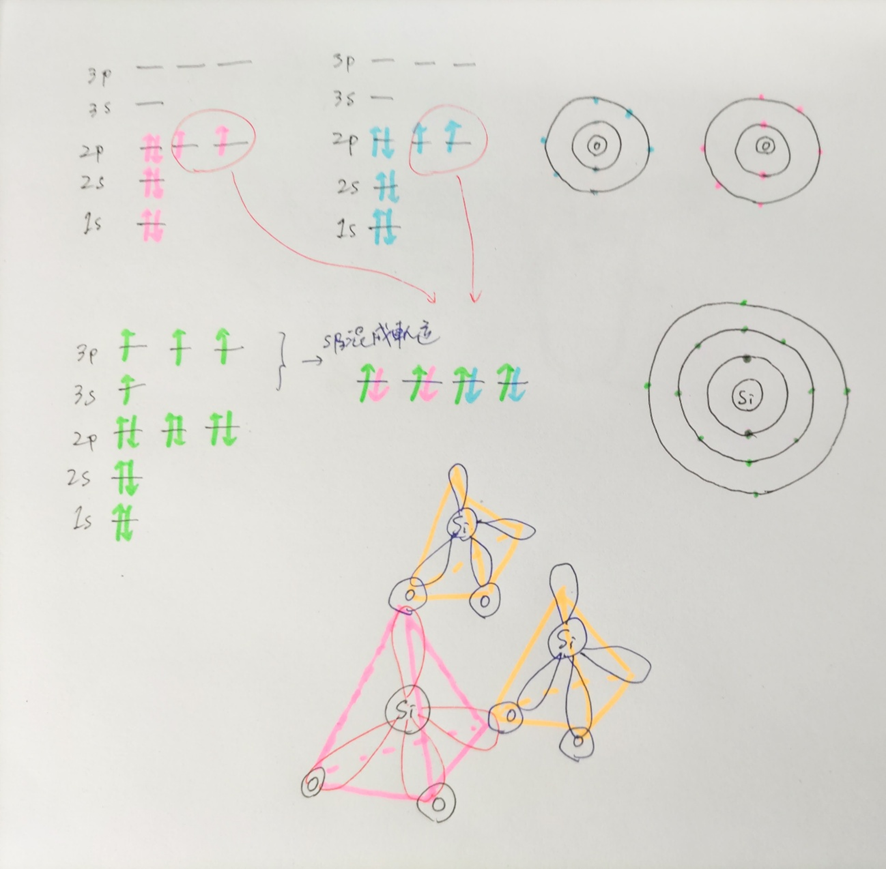
しかし、ガラス管の表面では、結合の相手がいなくなって正四面体の頂点が空席になっているSiO2分子が存在します。
この部分には空気中の水蒸気に含まれる水分子が結合し、Si-OH(シラノール基)が形成されます。したがって、ガラスは表面に多くのOH基を持つ親水性となります。
このOH基が液体分子と水素結合をつくるため、ガラス管の側面に濡れ広がります。
また、表面張力によって液面は縮まろうとする方向に力が加わっています。
そのため、毛管壁面に濡れ広がった液面が縮まろうとすることで、結果的に水面を持ち上げられます。
このように、壁面への付着力(濡れ)と表面張力の垂直成分が、液面を持ち上げる毛管上昇を起こす力の正体です。
そして、これらの力と液体の重さがつりあうまで液面は上昇していきます。
毛管の場合は管の半径が非常に小さいため、表面張力の効果が重力に対して相対的に大きくなり、したがって液面が比較的高く上昇するのです。
ただし、ひとつ注意しないといけないことがあります。
上記は水を主成分とする液体の話でしたが、液体や表面の違いにより、表面張力と濡れやすさの関係も変わってきますので、常に毛管上昇になるとは限りません。
例えば、水銀は水と違ってガラス面には濡れにくく、表面張力は水よりもはるかに大きくなっています。
水銀は金属であり、水銀原子同士が金属結合と呼ばれる強固な結合をつくるため、水銀同士の凝集力が非常に強いのです。
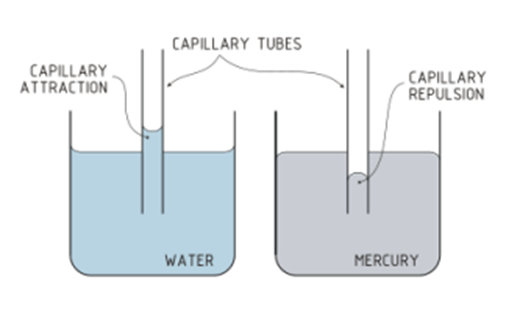
したがって、下図のように水はガラス管内で凹型のメニスカスを作りますが、水銀は上に凸型のメニスカスになります。
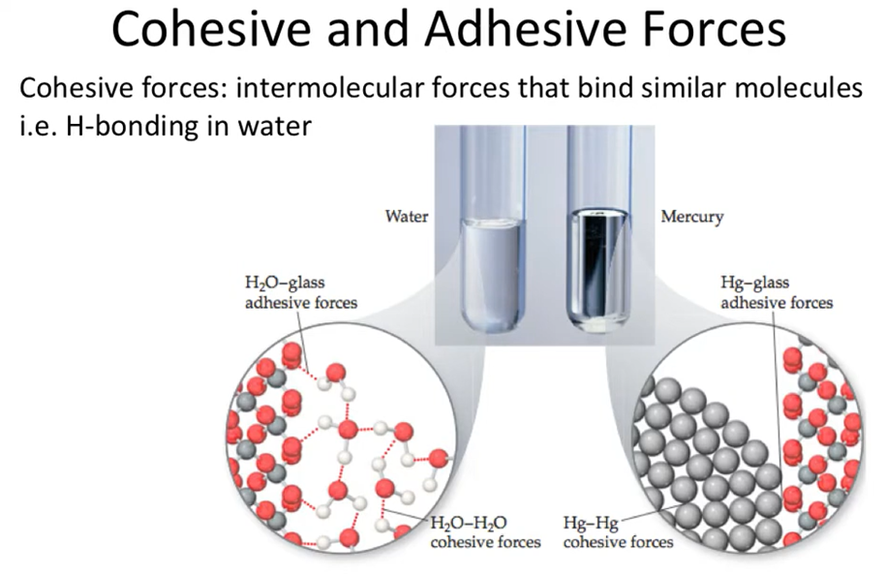
このような場合には、毛管上昇は起こらず、かえって毛細管内部の液面の方が周囲の液面よりも低くなります。
毛管上昇高さを求める
では、毛管上昇が起きる場合を考えて、液体はどれくらいの高さまで上昇するのでしょうか?
これには、毛管上昇高さを求める次の式が存在します。
毛管上昇高さを求める式:
H:上昇高さ
γ:表面張力
θ:接触角
ρ:液体密度
g:重力加速度
r:毛細管内径
なぜこのような式になるのかをみていきます。
まず、前提として、ラプラス圧というものがあります。
液体表面が曲率をもつ場合に、表面を横切る液体の内部と外部に圧力差が発生すると考えられ、これをラプラス圧と呼んでいます。
曲率とは、簡単に言うと曲線や曲面の曲がり具合のことで、半径 r の円周の曲率は 1/rと定義されています。
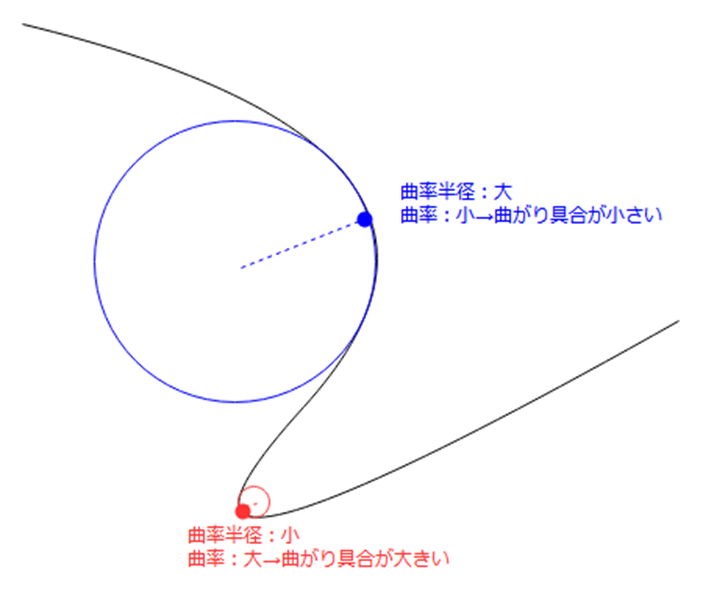
先ほど表面張力によって液面が球面になるという話をしましたが、液面が球面になるということは曲率が生じているということなので、このとき、液体の外側と内側の間では圧力差が生じているということになります。
表面張力は、表面の分子が内部の分子から引っ張られることで表面積を最小化しようとする現象ですので、このとき内側には外側よりも強い圧力が生じているとイメージできるかと思います。試験管の中では上に凸のメニスカスができている状態です。
反対に、毛細管表面に濡れ広がって凹型のメニスカスができているときは、液面内部の圧力よりも外部の圧力の方が高い状態です。大気の圧力で液面が押されてくぼんでいるようなイメージです。
ラプラス圧は、次の式で与えられます。
ラプラス圧:
γ:表面張力
R1、R2:液体表面の曲率半径
2つの半径がどの部分にあたるかですが、まず、液体界面上の任意の点について、この点を通る法線を考えます。法線とは、その点における接線と直交する直線です。
液体表面のある点において、その点を通る接線に垂直な2つの直交平面を考えます。それぞれの平面と液面が交わる曲線に沿って円を仮定し、その半径を R1、R2 とします。
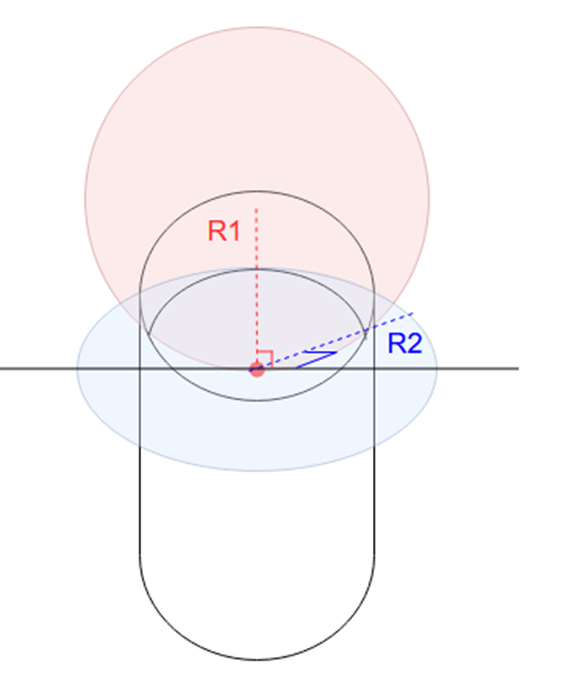
ただし、決まり事として、円の中心が液体内部にあるときは曲率半径の符号を正に、外部にあるときは負に取ります。
親水性表面に対する水のような場合、円筒を横から見た時に凹型のメニスカスとなりますので、円の中心は液体外部に位置します。したがって、曲率半径は負符号になります。
表面張力γは正の定数ですので、この場合、ラプラス圧は負になります。
通常の液体では、毛細管の内側にできる液面は下に凹んだメニスカスを形成し、このとき液面の曲率半径は負になります。
ラプラス圧は、液体の内部と外部の圧力差(⊿P = P内 − P外)を表すものであり、表面張力 γ が正で、曲率半径が負の場合、ラプラス圧も負になります。
これはすなわち、液体内部の圧力が外部よりも低いことを意味します。このような負のラプラス圧が、外部から液体が引き込まれる毛細管現象などの駆動力となります。
このように、実際の符号は液面の形状によって決まりますが、以降は計算の都合上、ラプラス圧や曲率半径を絶対値符号つきで扱うことにします。
表面張力でできる液面は理想的には球状になるため、上記のラプラス圧の式は、R1=R2=Rと置き換えて、下記のようにあらわせます。
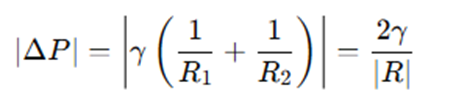
・・・・①
つづいて、毛細管表面と液体との接触角とθとすると、毛細管の断面は下図のようになります。
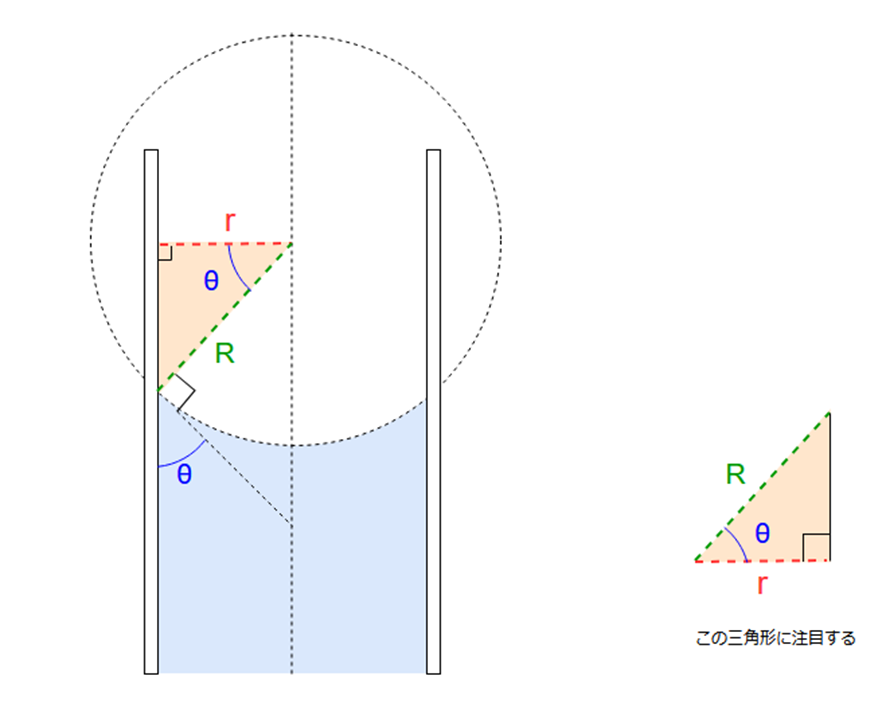
この図に注目すると、接触角θを用いて、毛細管の内径rと液面の曲率半径Rの間に以下の関係が成り立ちます。
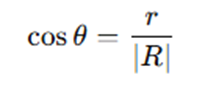
・・・②
続いて、圧力の関係を考えてみましょう。
ここで、下図のように、毛細管内の液面直上の気体圧力p、液面直下の液体内圧力q、毛細管外の液面と同一の高さにある点での圧力をp0とします。
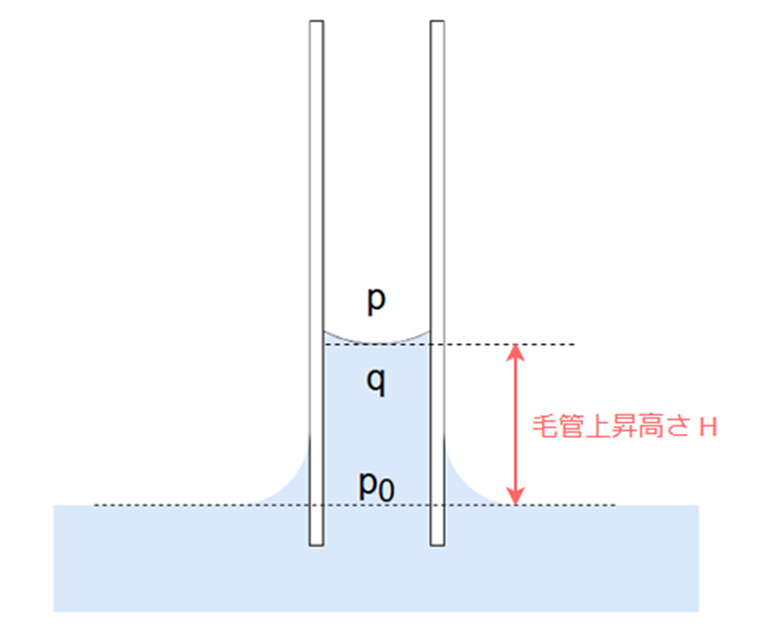
毛細管外の液面は曲率が生じていないので、p0は大気圧と同じとみなせます。
また、これは圧力pと等しくなります。
p=p0 ・・・③
さて、ここでqとp0の間の圧力差を調べます。
qは、毛細管内の液面における圧力であり、これは基準面(p0の位置)より、高さH(毛管上昇高さ)だけ上にある点の圧力です。
水の深いところでは水圧が高いということは感覚的にもわかるかと思いますが、深いところではその上にある水の重さを受けているため、より圧力が高くなります。
「重さ」とは、物体に働く重力の大きさのことであり、圧力とは単位面積あたりにはたらく力のことです。
したがって、ある水深での圧力に、基準面からの水の重さを単位面積で割った力を足すと、基準面での水圧が求められます。
ただし、密度が関係するため、密度ρを用いて、差分の圧力はρgHとなります。
したがって、qとp0の間には、次の関係式が成り立ちます。
q+ρgH =p0
これと③より、
q+ρgH=p
すなわち、
p-q=ρgH ・・・④
また、ここで、p(液面外部)とq(液面内部)の圧力差(q-p)がラプラス圧となります。
凹型メニスカスの場合、p>qとなるため、0>q-p、よってラプラス圧は負の値となります。
①と④より、
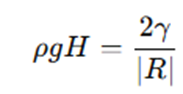
・・・⑤
さらに②と⑤からRを消去して変形すると、最初に示した毛管上昇高さの式が導かれます。
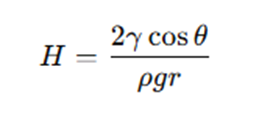
Bio-Rad社の特許(WO2014205447A2)より
前回記事で取り上げたBio-Rad社の特許(WO2014205447A2)は、ddPCRにおいて、毛細管現象と圧力差の関係を利用して、外部の液滴生成装置やバルブを使わずに、簡便な液滴生成システムを実現したというものでした。
原文の内容解説
その部分の原理を説明した箇所を抜き出してみていきたいと思います。
When a tube is in contact with a fluid (e.g., sample fluid 64) in a reservoir (e.g., well 68), gravity may limit the ability of the fluid to travel up the tube. The capillary rise height H depends on the tube inner radius r, the surface tension γ of the fluid at a liquid-air interface, the density of the fluid ρ, and the contact angle θ of the fluid on the tube surface, according to the following formula:
Provided that the capillary rise height is less than the height difference between the fluid in the well and a channel 74 above the well, gravity will ensure that the fluid cannot reach the channel without application of a driving force, such as a pressure differential. Accordingly, the fluid is retained in the well until the driving force is applied.
・・・(略)・・・
In some cases, the volume (e.g., the well) into which the tube extends may be closed instead of vented, increasing the retention power of the structures described above. Any capillary rise would be counteracted by an increase of back-pressure in the closed volume, further isolating the fluid in the well from channel 74 above.
前半部分は、先ほど式の導出について説明した毛管上昇高さに関する記述です。
添付図面の左側に注目すると、試料液がウェルの中にたまっており、そこにチューブが立てられています。
毛管上昇高さは先ほどの式によって決まり、液体の表面張力と毛細管壁面への付着力によってある一定の高さまでは上昇しますが、ずっと上昇し続けるわけではなく、重力とのつりあいによって、ある高さで止まります。
したがって、さらに何か別の力を加えない限りは、重力によってある一定の高さで上昇が抑えられるということを説明しています。
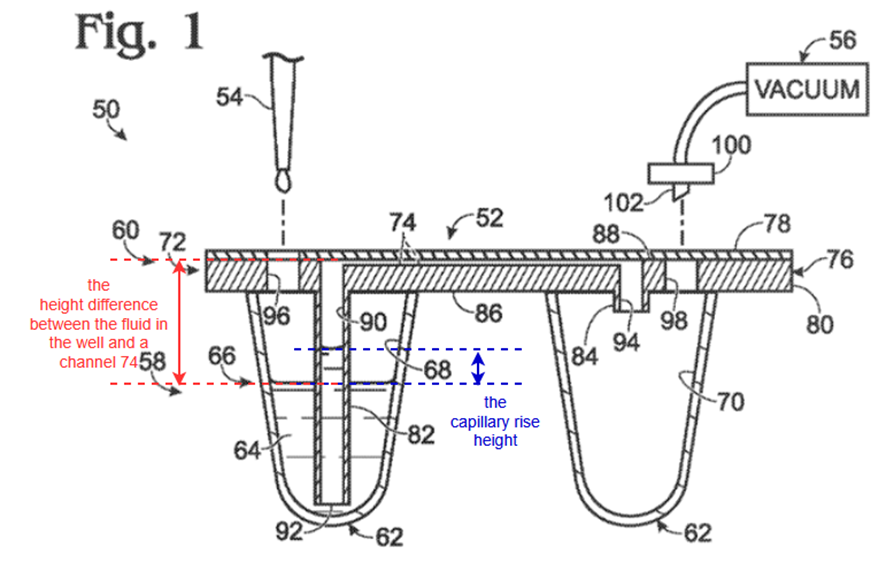
そして、上の図に青い線で書き入れた毛管上昇高さが、赤い線で書き入れた液体とチャネル74との距離よりも小さければ、外部の力なしでは試料液はチャネルに流入しないということを言っています。
外部の駆動力として挙げられている圧力差は、図の符号56で示されている真空装置によってもたらされます。
真空装置によって液面上部を真空にすることで、圧力差により試料液がチャネル74に流入するようになります。
真空状態というのは、理想的には全ての気体分子が存在しないような状態です。実際にはすべての分子を排除することは困難ですが、通常の大気の状態よりも非常に気体分子が少ない状態になっています。
圧力は、気体分子が飛び回って壁にぶつかる際に、その壁を押す力と説明されます。
分子が少なければその分、分子が壁(ここでは液体との界面)を押す力も弱くなるので、真空では非常に圧力が小さい(理想的にはゼロ)ということになります。
ラプラス圧について説明したように、真空状態にする前は液面内部の方が液面外部よりも圧力が小さく、凹型のメニスカスができています。ここで真空状態を作り出し、大気側から液面を抑える力が弱まれば、その分液体内部の圧力の方が大きくなりますので、液面はより上昇することができるようになります。
したがって、必要な時だけ圧力差を与えれば、バルブを使わなくても簡単に液滴生成を制御することができるというわけです。
このように数式などを使って説明すると難しいようですが、非常に簡単に言えばストローの原理です。
ジュースを入れたコップにストローを挿して、それだけでジュースがストローの上端まで吸い上げられてこぼれてきてしまったら大変ですが、実際には重力との関係でそこまでジュースは上昇しません。
しかし、ストローの先に口をつけて吸い込めば、ジュースはストローの上端まで上がってきて口の中に入ります。これは、ストローの空気を吸い込むことでストロー内の空気分子を少なくし、圧力差を作り出すことによる同様の現象です。
後半の文章では、試料液を貯めているウェルを密閉状態にすることで、背圧により液体の上昇をさらに抑えることができるということを述べています。
背圧とは、流体の流れに対して反対向きにかかる圧力のことです。ここでは、毛管現象により液面が上昇する方向に対し、それを抑え込むように下向きにかかる圧力を指しています。
なぜウェルを閉じることでこのような背圧が生じるのでしょうか。
先ほど、圧力は気体分子が壁を押す力だと書きました。
ここで、ウェルが閉じられるということは、気体分子がより狭い空間に閉じ込められることを意味します。
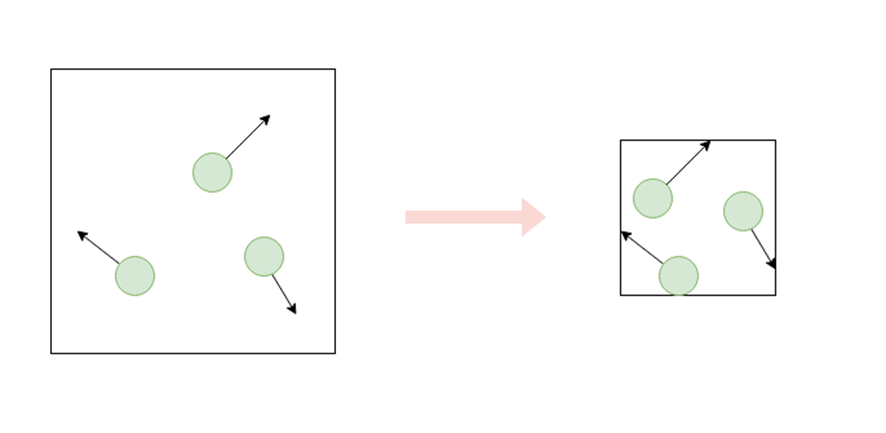
同じ数の分子であっても、狭い空間であればそれだけ壁にぶつかりやすくなりますので、単位面積当たりの壁を押す力は大きくなります。
したがって、ウェルを閉じることで液面上部の大気の圧力は上昇し、より確実に液体をウェル内に抑えこむことができるということです。
試訳
最後に、原文・公開訳・私の考えた訳を並べます。
【原文】
When a tube is in contact with a fluid (e.g., sample fluid 64) in a reservoir (e.g., well 68), gravity may limit the ability of the fluid to travel up the tube. The capillary rise height H depends on the tube inner radius r, the surface tension γ of the fluid at a liquid-air interface, the density of the fluid ρ, and the contact angle θ of the fluid on the tube surface, according to the following formula:
Provided that the capillary rise height is less than the height difference between the fluid in the well and a channel 74 above the well, gravity will ensure that the fluid cannot reach the channel without application of a driving force, such as a pressure differential. Accordingly, the fluid is retained in the well until the driving force is applied.
・・・(略)・・・
In some cases, the volume (e.g., the well) into which the tube extends may be closed instead of vented, increasing the retention power of the structures described above. Any capillary rise would be counteracted by an increase of back-pressure in the closed volume, further isolating the fluid in the well from channel 74 above.
【公開訳】
チューブが、貯槽(例えば、ウェル68)内の流体(例えば、試料流体64)と接触しているときに、重力は、流体がチューブを遡る能力を制限し得る。毛細管上昇高さHは、以下の公式により、チューブの内側半径r、液体空気界面における流体の表面張力γ、流体の密度ρ、およびチューブの表面上の流体の接触角度θに依存する。毛細管上昇高さは、ウェル内の流体とウェルの上のチャネル74との間の高さの差より小さい場合に、重力は、圧力差などの推進力の印加なしでは流体がチャネルに到達し得ないことを確実にする。したがって、流体は、推進力が印加されるまでウェル内に保持される。
・・・(略)・・・
いくつかの場合において、チューブが貫入する体積(例えば、ウェル)は、穴をあけられる代わりに閉じられ、上で説明されている構造の保持力を高めることができる。毛細管上昇は、閉じられている体積内の逆圧の増大による反対の作用を受け、上のチャネル74からウェル内の流体をさらに隔てる。
【自分の訳】
チューブが貯液槽(例えば、ウェル68)内の流体(例えば、試料流体64)と接触しているとき、重力によって、その流体がチューブ内を上昇する力は制限され得る。毛管上昇高さHは、以下の式によって、毛管内径r、液界面における流体の表面張力γ、流体の密度ρ、および毛管表面に対する流体の接触角θによって決まる。毛管上昇高さが、ウェル内の流体とウェル上方に位置するチャネル74との高さの差よりも小さい場合には、駆動力(例えば、圧力差)が加えられない限り、流体がチャネルに到達することは重力によって確実に阻止される。したがって、駆動力が加えられるまでは、流体はウェル内に保持される。
・・・(略)・・・
場合によっては、チューブが延在する空間(例えばウェル)は、通気されずに密封されていてもよく、これにより、上記構造における保持力が向上する。密封空間内では、背圧の上昇によって毛管上昇が打ち消され、ウェル内の流体は上部のチャネル74からさらに隔てられることになる。
参考
・類家正稔「基礎 界面とコロイドの化学」(東京電機大学出版局、2024年1月)
・協和界面科学株式会社サイト「界面科学の世界」
・渡辺正「表面張力のしくみ」(化学と教育、47巻、9号、1999年)
・公益社団法人高分子学会サイト「表面張力(Surface Tension)測定」
・三洋貿易株式会社サイト「表面張力・界面張力とは?」
・日本ガイシ株式会社サイト「毛細管現象 容器の中から逃げ出す?水!」

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4af6cb8e.be139a42.4af6cb8f.6bbda93f/?me_id=1351260&item_id=10003711&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fpit-life%2Fcabinet%2Fzakka%2Fco%2Fpit001-01.jpg%3F_ex%3D240x240&s=240x240&t=picttext)


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4af7a995.4a5239ef.4af7a996.c0537ef8/?me_id=1382640&item_id=10000690&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Flife-care%2Fcabinet%2Fimg%2F09836651%2F2856-000530.jpg%3F_ex%3D240x240&s=240x240&t=picttext)





![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4a47823f.ec7d24f1.4a478240.065a96b7/?me_id=1213310&item_id=21127378&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F4902%2F9784501634902_1_122.jpg%3F_ex%3D240x240&s=240x240&t=picttext)









コメントを残す