比表面積測定法

前回の記事で研磨用スラリーの特許について書きました。
その特許の中に、シリカ砥粒の粒子径と比表面積の測定に関する記述がありましたので、今回は比表面積から粒子径を求める方法についてまとめました。

概要

比表面積とは

比表面積とは一般に、単位量あたりの粉体中に含まれる全粒子の表面積の総和を指します。

例えば、クッキーを作るときに200gの小麦粉を量り取るとします。
その中には小さな小麦粉の粒がいくつも含まれています。
これらの表面積の総和が比表面積です。

ただし同じ小麦粉200ｇでも、粉の目が比較的大きな強力粉と比較的小さな薄力粉とでは、比表面積は異なります。

比表面積はなぜ重要か

粉体の特性を考えるには粉体を構成する粒子の性質を考えないといけませんが、他の物質と粒子の間に働く様々な化学的・物理的作用は表面で起きています。

そのため、粉体の性質を考えるうえで粒子の比表面積を知るということは重要になるのです。

粒子径と比表面積との関係

特許明細書の記述

特許明細書には以下の記述があります。

シリカ砥粒の１次粒子の平均粒子径は、以下のようにして測定することができる。
  すなわち、シリカ砥粒の１次粒子の平均粒子径は、シリカ砥粒の１次粒子を真球状と仮定し、下記（３）式により算出する。なお、下記（３）式において、シリカ砥粒の密度は、２．２ｇ／ｃｍ^３とする。
    ｄ＝６／ρＳ  ・・・（３）
      ｄ：一次粒子径（μｍ）
      ρ：シリカ砥粒の密度（ｇ／ｃｍ^３）
      Ｓ：比表面積（cｍ^２／ｇ）
【００２４】
  上記（３）式における比表面積は、比表面積・細孔径分析装置ＱＵＡＤＲＡＳＯＲＢ  ｅｖｏ（Ｑｕａｎｔａｃｈｒｏｍｅ  Ｃｏ．製）を用いて、ＪＩＳ  Ｚ８８３０：２０１３（ガス吸着による粉体（固体）のＢＥＴ比表面積測定方法）により測定する。なお、シリカ砥粒としては、８５℃で２４時間真空乾燥したものを用いる。以下に、詳細な条件を示す。
    前処理：シリカ砥粒を測定セルに入れ、８５℃で２時間真空脱気する。
    測定原理：定容法
    吸着ガス：窒素ガス
    測定温度：７７．３５Ｋ（－１９５．８℃）
    セルサイズ：スモールセル  １．５ｃｍ^３（ステム外径９ｍｍ）
    測定項目：Ｐ／Ｐ_０＝０～０．３の吸着側数点
    解析項目：ＢＥＴ多点法による比表面積

明細書のこの記述を見ると、シリカの粒子径を求める前提として比表面積を求めているということが分かります。

粒子径と比表面積の関係式

明細書にある以下の関係式がどのようにして導かれるのかを考えてみましょう。

    ｄ＝６／ρＳ 
　    ｄ：一次粒子径（μｍ）
      ρ：シリカ砥粒の密度（ｇ／ｃｍ^３）
Ｓ：比表面積（cｍ^２／ｇ）

一次粒子というのは、粉体やゾル中での粒子の最小単位のことです。それに対して二次粒子というのは一次粒子が凝集した状態のものです。

二次粒子のように粒子がいくつも集まって凝集している状態では比表面積の議論をするのは困難です。そのため、個々の粒子がバラバラになっている一次粒子の状態を考えます。

「１次粒子を真球状と仮定」というのは、実際の粒子の形は真球状ではなく、多少歪みがあるためです。ただそれだと議論が難しくなってしまうので、計算を簡単にするために真球状であると仮定して、その球の直径を粒子径とするのです。

球の体積は、半径をrとして一般に次の式で表されます。

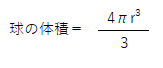
そこで粒子1個の体積V´について考えると、一次粒子径d は球の直径とみなせますので、r=d/2が成り立っています。
これを上の式に代入すると、次の式が得られます。

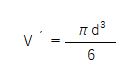
これは粒子1個分の体積なので、1gあたりに含まれる粒子の個数をNとすると、体積の総和VはV´にNをかけて、次の式で表せます。

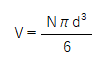
すると体積Vは密度ρを使って1/ρ＝Vと表せますので、次の式が成り立ちます。

また、一般に球の表面積について以下の式が成り立ちます。

　球の表面積＝4πr²

粒子1個の表面積S´とすると、r=d/2を代入して次の式が得られます。

　S´＝πd²　　

これは粒子1個分の表面積なので、先ほどと同様に1gあたりの粒子の個数Nをかけることで表面積の総和（比表面積）Sを次の式で表せます。

　S＝Nπd²　　　・・・②

ここで先ほど①式を使って①÷②をすると、次の式になります。

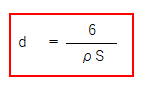
明細書に示されていた式（ｄ＝６／ρＳ）が導けましたね。

また、
　密度ρの単位：ｇ／ｃｍ^３
　比表面積Sの単位：cｍ^２／ｇ
ですので、
両辺の単位も長さの単位でそろっていることが確認できます。

さて、このようにして粒子径と比表面積の関係式が得られたところで、今度は観測データから比表面積を求め、これを先ほどの式にあてはめて粒子径を求める、というのが明細書に書かれている方法です。

比表面積の測定方法

小麦粉の例では適当に200gと書きましたが、粒子はマイクメートル単位と非常に小さいため、実際に比表面積を求める際は通常1gあたりの粉体中に含まれる全粒子の表面積の総和（単位：cm²/g）で表されます。
もしくは1cm³あたりの比表面積として（単位：cm²/ cm³）で表されます。

今回は明細書にならって1gあたりの粉体を基準に比表面積を考えていきます。

比表面積の測定法には大きく分けて透過法とガス吸着法というものがあります。

透過法とは、粒子が充填されているところに水や空気などの流体を流す時、粒子が細かいほど流れにくくなることを利用して粒子の比表面積を求めるというものです。

ガス吸着法は、ガス吸着法とは、大きさが既知の分子を調べたい粉体粒子の表面に吸着させ、その量から資料の表面積を調べる方法です。

ガス吸着法の種類

ガス吸着法では比表面積を求めるために、試料へのガス分子の吸着量を測定します。
吸着量の求め方によって、重量法、流動法、容量法、の3種類に大別されます。

重量法は、測定前後での資料の重さを量り、その変化量からガス分子の吸着量を求める方法です。原理が理解しやすく、高価な装置も必要としませんが、吸着質ガスの温度と圧力の管理が難しく、精度の面では劣ります。

流動法は、吸着ガスをHeなど不活性のキャリアガスとともに試料に流通させ、出口での吸着ガスの濃度変化を測定することでガス分子の吸着量を求める方法です。ガスクロマトグラフィーと同様の手法です。

容量法は、その中でも最も一般的な方法で、吸着前後のガスの状態変化から吸着量を求める方法です。高価な装置が必要になりますが、精度が高いのがメリットです。

容量法にはさらに、定容法と定圧法の2種類に分けられます。

定容法は、測定温度と吸着装置の特定部分の容積を一定にしておいて圧力を変化させ、ガス導入時の圧力と吸着平衡時の圧力の差から吸着量を求める方法です。

定圧法は、測定温度と吸着質ガスの圧力を一定に保った状態でガスの容積がどれくらい減少するかを測定して吸着量を求める方法です。

いずれの場合も、理想気体の状態方程式（PV=nRT）を利用します。

測定装置として明細書に示されているＱＵＡＤＲＡＳＯＲＢ  ｅｖｏは下図の装置です。

1つの装置の中に全部で4つの容器が入っており、1つの測定が終わるとすぐ別の測定が開始できるというのがメリットです。

1つ1つの容器は以下のようになっています。

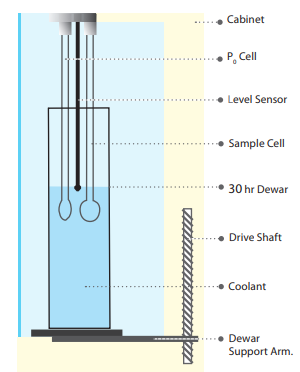
これは定容法を用いる測定装置で、測定手順は以下の通りです。

1.　窒素ガスをためておく管（左）と、試料粒子を入れる管（右）があります。状態方程式（PV=nRT）を使って測定前の窒素のモル数を求めておきます。
2.　ある一定圧力で窒素ガス管に窒素ガスを送り込みます。
3.　2つの管をつなぐバルブを開けて、窒素ガス管から試料管へ窒素ガスを移動させます。
4.　2つの部屋が平衡状態になったときの窒素のモル数を状態方程式から算出します。
5.　測定前後のモル数を比較して吸着量を求めます。

測定の前処理

試料のシリカを事前に真空乾燥させておくのは、シリカ表面についている不純物や水分を除去しないと、シリカ粒子以外のものとの吸着が関係してきてしまい、正確な測定ができなくなるためです。そのため、高い温度で試料に含まれる水分などを除去します。
その後、試料を冷やして低温状態にします。

また、吸着量は吸着質の種類と温度によっても変わってくるため、どのような条件で測定したのかを示す必要があります。
測定温度の77.35Kというのは液体窒素の沸点です。この温度における窒素の占有面積（窒素分子が粒子表面に吸着したときに1個の窒素分子が占める表面積）は0.162 nm²であることが分かっているため、この値を使って比表面積を求めることができます。この値を使った比表面積の求め方については後述します。

ガス吸着法の理論

ガス吸着法とは、大きさが既知の分子を調べたい粉体粒子の表面に吸着させ、その量から資料の表面積を調べる方法です。
比表面積の測定方法として特によく使われる方法です。

ガス吸着法では、試料を冷却した後、窒素ガスのように試料と反応を起こしにくいガスを吹き込み、試料表面にガス分子を吸着させます。

吸着には物理吸着（ファンデルワールス力などの弱い分子間力による吸着）と化学吸着（化学結合による吸着）が考えられ、どちらも一緒に起きている場合もありますが、「試料と反応を起こしにくいガス」を選択しているので物理吸着がメインになります。

前処理の段階で「試料を冷やす」と書きましたが、これも物理吸着で重要なポイントになります。
熱を加えた状態では分子の動きが活発になり、個々の分子がバラバラな運動をしようとするので、ガスの吸着が起こりにくくなってしまいます。
そのような状態では測定ができないので、資料を冷やして吸着が起こりやすい状況を作る必要があるのです。

吸着には吸着するもの（吸着質）と吸着されるもの（吸着媒）が存在し、ガス吸着法の場合は試料粒子が吸着媒、窒素ガスが吸着質、ということになります。
吸着媒の表面に吸着質が物理的相互作用あるいは化学結合により、その部分の吸着質の濃度が他より高くなる吸着現象です。

また物理吸着の場合は比較的弱い相互作用によって吸着質が吸着媒にくっついている状態なので、くっついたり離れたりが可逆的に起こります。
吸着とは反対に吸着質が吸着媒から離れていくことを脱着と言います。

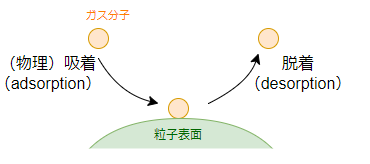
可逆的ということは、吸着と脱着が同時に起きていて、それぞれの速度が等しくなる平衡状態が存在します。
粒子表面に吸着できる分子の数には上限があり、その最大量に達したとき（この時の被覆率を最大被覆率という）に平衡状態になります。

最初は粒子表面への吸着が進み、その間に脱着も起こりますが、吸着速度の方が速いために吸着現象が進み続けます。しかし、ある程度まで吸着が進むとそれ以上吸着が進まない飽和状態に達し、このときには吸着速度と脱着速度が等しくなる平衡状態になり、見かけ上吸着が止まります。
ミクロで見れば吸着と脱着が起きていますが、両者の反応速度が等しくなるので出入りが同じになり、全体として吸着は起きていないように見えるというわけです。

Langmuir（ラングミュアー）吸着式

ガスが粒子の表面に物理吸着するとき、どのように吸着していくかについてもう少し考える必要があります。
アメリカの化学・物理学者ラングミュアーが考えたのは、粒子の表面にガス分子が単層で吸着するというモデルです。

ラングミュアーは以下の前提に立って、最大被覆率を求める式を考えました。

・吸着媒には有限な数N の吸着サイトがあり、そこにだけ吸着質分子が吸着する。
すべての吸着サイトは等価である。
・1つの吸着サイトには1つの吸着質分子しか吸着しない。
・1つのサイトにおいて、吸着質Ｍと吸着媒Ｓ、吸着後の状態ＭＳの間に、Ｍ+Ｓ⇌ＭＳの平衡・状態が生じる

これらの前提で、被覆率θについて次の式が成り立つとしています。

ラングミュア―の吸着等温式：

被覆率というのは、占有されている吸着サイトの数を吸着サイトの総数で割ったもので、どれくらい吸着サイトが吸着質分子で表されているかを表す割合です。

ラングミュア―のモデルでは、下図のようにN_S個の吸着サイトと、N_A個の吸着分子があり、各吸着サイトに1つずつの吸着質分子が吸着できるとしています。

ここで吸着速度をν₁、脱着速度をν₂とします。

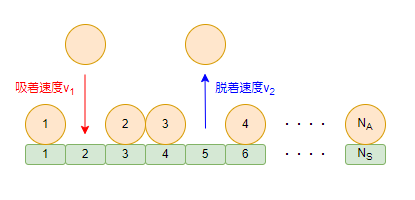
吸着速度ν₁について：
吸着速度はまだ吸着されていない（空席状態の）吸着サイトの数（N_S-N_A）に比例します。また、圧力が高くなって吸着質分子と粒子表面の接触が起こりやすくなるほど吸着も起こりやすくなるため、吸着速度は圧力にも比例します。

そこで圧力をp、比例定数をkとおくと、次の式が成り立ちます。

ν₁＝kp（N_S-N_A）　　　・・・①

脱着速度ν₂について：
脱着はすでに吸着しているサイトから吸着質分子が離れていく現象なので、すでに吸着している分子の数N_Aに比例します。

そのため比例定数をk´とおくと、次の式が成り立ちます。
　
　ν₂＝ｋ´N_A　　　・・・②

吸着と脱着が平衡状態にあるときは
　
　ν₁＝ν₂

が成り立つため、①と②式より、

　kp（N_S-N_A）＝ｋ´N_A

これをＮ_Ａについてまとめると、

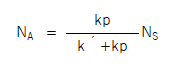
右辺の分母と分子をk´で割って、

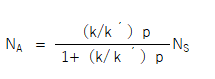
k/k´を定数aとおくと、

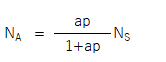
さらに両辺をN_Sで割ると、

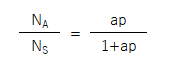
N_A/N_S は、N_Sの吸着サイトをN_Aの吸着質分子が占めている割合を表しますので、N_A / N_Sを被覆率θとして、最終的に次の式が得られます。

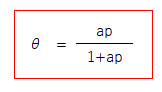
これがラングミュア―の吸着等温式です。

BET吸着式

ラングミュアーの式は1つの吸着サイトに1つの吸着質分子が吸着する単層のモデルを考えていましたが、実際にはそうではなく、吸着質分子の上にさらに吸着質分子が吸着するような多層構造になるはずだと考えたのがＢＥＴモデルです。

ガス吸着法の中でも特によく使われる方法で、今回取り上げている特許明細書でもＢＥＴ吸着法による測定が使われています。

「BET」は開発に携わったブルナウアー（Brunauer）、エメット（Emmett）、テラー（Teller）の3名の頭文字を取って名付けられました。

BETモデルでの吸着は以下のように進行します。

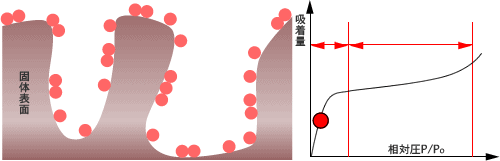
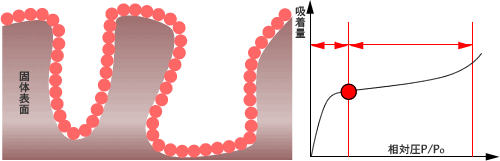
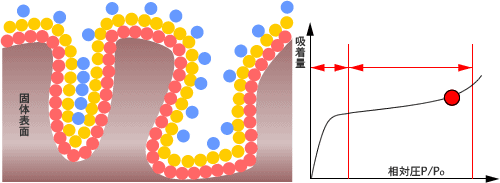
初めはラングミュアーのモデルと同様に単層ができますが、さらに吸着質分子同士の相互作用により、一つの吸着サイトに多数の吸着質分子が積み重なって多層構造が出来上がります。

ＢＥＴ吸着等温式は以下のように表されます。

Cは吸着熱に関する定数を表しています。
この式を使ってどのように比表面積を求めるのかについては後述します。

吸脱着等温線

吸着が起こるには、まず吸着質が吸着媒にぶつかって相互作用を起こす必要があります。
そして、空間内にたくさんの吸着質が存在した方が、吸着質が吸着媒にぶつかる確率が高くなると考えられます。
そのような状況は、ある一定の温度であれば、圧力を高めることによって作り出すことができます。

そこで、一定温度で圧力を変化させたときの吸着量の変化をグラフで表したものが吸脱着等温線です。
先ほどBETモデルの図に書かれていたグラフです。
横軸に相対圧（Ｐ/Ｐ₀）、縦軸に吸着量をとってプロットします。


相対圧（p/p₀）のpは絶対圧、つまり絶対真空（完全な真空状態）を基準0Paとして表した現在の圧力のことで、p₀は吸着質の飽和蒸気圧、つまり液体と気体が平衡状態にあり、これ以上圧力をかけると気体から液体に凝縮するという圧力を表しています。

p/p₀＝1になるときにはp=p₀、つまり現在の圧力が飽和蒸気圧に一致するということになりますので、p/p₀が0から1に近づいていくにつれて吸着質の凝縮が起こりやすくなります。

飽和蒸気圧は物質により異なるため、複数の吸着質を用いて測定結果を比較したいような場合、単純に絶対圧pだけを使っての比較はできません。そのため飽和蒸気圧p₀で除した相対圧で表すのが一般的です。

吸着の段階は多層的に進みますが、比表面積を算出するには単分子層の吸着量を読み取る必要があります。
そのため、グラフの最初の直線的な傾きが続く範囲内における観測データをBET式に当てはめることで、吸着量を正確に測定して比表面積を算出します。

細孔分布

先ほど書いた飽和蒸気圧の定義からするとpの値がp₀を超えたときに凝縮が始まるということになりますが、実際には飽和蒸気圧より低い圧力でも凝縮が起こることがあります。
これは毛管凝縮と呼ばれる現象です。

粒子の表面にはいくつもの細かな空孔があり、以下のように分かれています。

　ミクロ孔：2nm以下、メソ孔：2～50nm、マクロ孔：50nm以上

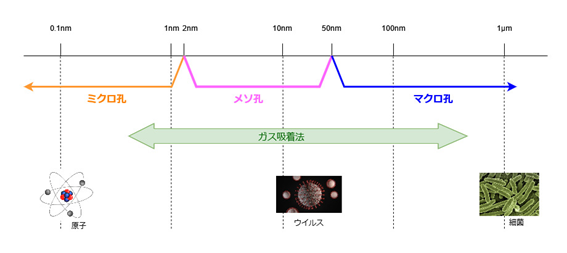
吸着質がその空孔の中に入っていくと、狭い空間では分子同士の接触が増え、相互作用が強くなることで、通常よりも低い圧力で凝縮が起こりやすくなるため、毛管凝縮が起こるのです。

凝縮が起きるときには吸着量の増え方が一気に上がりますので、吸脱着等温線のグラフの傾きに注目するといつ凝縮が起きたかを確認することができます。

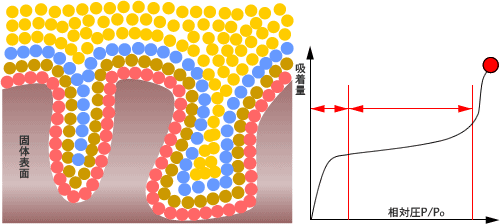
そのため、BET法では比表面積だけでなく細孔分布についても測定することが可能です。

比表面積の計算方法

一点法と多点法

比表面積を求める際は、観測データから得られる結果をBET式に当てはめます。

この際、ある一点の相対圧（通常はp/p₀が0.3～0.35の範囲のある一点）での吸着量の観測データのみを使用する方法を一点法といいます。

一方、いくつかの相対圧において吸着量を観測しプロットするのが多点法です。
吸脱着等温線は吸着過程（圧力を上げていく過程）と脱着過程（圧力を下げていく過程）の両方を含むため、「測定項目：Ｐ／Ｐ_０＝０～０．３の吸着側数点」というのは、圧力を上げていく吸着過程において測定した、相対圧0～0.3の範囲におけるいくつかの点で吸着量を観測した、という意味になります。

多点法の方が多くのデータを使って算出するので精度は高いため、より精度の高い結果を得たい場合は多点法が使われます。

一方で一点法でも相対圧0.3～0.35の範囲のある一点と原点とを結んでできる直線と、多点法で得られるグラフを比べてもその誤差はおおむね5％以内だとされているため、それほど精度を必要とせず、迅速に結果を得たい場合には一点法が使われます。

具体的な計算例

では、観測データからどのように比表面積を導くのかを、例を使って計算してみましょう。

先ほど見たBET等温吸着式の両辺の逆数を取って、さらに両辺にp/(1-xp)をかけると、以下の式が作れます。

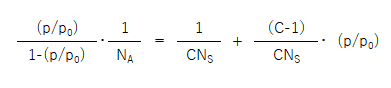
この式を次のようにx,y,a,bで置き換えてみると、一次関数y=ax+bの直線になります。

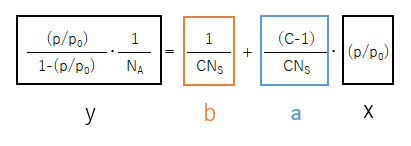
つまり、この式の中に測定結果から得られるpとN_Aの値、既知の値p₀を代入してプロットし、その点を結んでいくと縦軸y、横軸x、傾きa、切片bのグラフが書けるというわけです。

類家 正稔「基礎　界面とコロイドの化学」東京電機大学出版局の演習問題を参考に測定データをプロットしてみます。

75Kにおける窒素ガスを圧力pで試料粒子に吸着させたときの吸着量N_Aについて、以下のようなデータが得られたとします。75Kでの窒素の飽和蒸気圧p₀は76.0kPaとします。

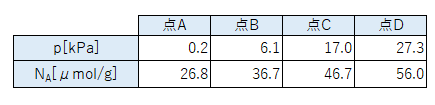
先ほどの式に上記のデータを当てはめて計算し、点A～Dをプロットしてみると下のようなグラフになりました。
ちなみにグラフはGeoGebraの無料で使える関数グラフを使って作図しました。

このグラフの傾きと切片の値を、先ほどの式のaとbにそれぞれ代入すると、Ｎ_ＡとＣの値が求められます。
傾きは0.02741、切片は0.00009だったので、代入すると以下の値になります。

　Ｎ_Ａ＝36.3μmol/g、
　Ｃ＝305

では、最後に試料粒子の比表面積Ｓを求めましょう。

Ｎ_Ａ＝36.3μmol/gより、1gあたりの窒素分子の数は、

　36.3×10^-6×6.02×10²³
　＝2.19×10¹⁹

窒素分子の占有面積は0.162 nm²であることがわかっていますので、上で求めた粒子の数に0.162 nm²をかけて、
　
　2.19×10^19×0.162
　＝3.55×10¹⁸nm²/g
　=3.6ｍ²/ｇ

よって、この観測データで求められる試料粒子の比表面積は3.6ｍ²/ｇということがわかります。

事前にわかっている粒子の密度と、ＢＥＴ法で求められる比表面積の値を、粒子径と比表面積との関係式（ｄ＝６／ρＳ）に当てはめれば粒子径が求められるということになります。

BET式の導出は数学の知識が足りず理解できなかったので数学を勉強してからまた考えてみます。
BET法以外の測定方法についてはまだきちんと調べきれていないので追加で調べます。
また細孔に関しては表面張力や多孔質材料の応用ともつながっていることがわかったので特許も探しながら整理します。

参考）
・島津製作所“粉博士の優しい粉講座” https://www.an.shimadzu.co.jp/service-support/technical-support/analysis-basics/powder/lecture/beginner/b11/index.html (参照2024-08-27)
・笛田・山田技術士事務所 “合成シリカと表面積” https://ce-fuedayamada.com/1169/ (参照2024-08-28)
・荒川 正文「粉体の比表面積測定法―主として測定法とその理論―」色材 Vol.44, 1971
・鷲尾 一裕「粉体表面物性測定技術 ガス吸着法∼水銀圧入法」日本画像学会誌 Vol.46, No.6, 2007
・類家 正稔「基礎　界面とコロイドの化学」東京電機大学出版局, 2024

8/27（火）学習時間：4.5H
・橋本の物理（26）～（28）
・1440　得意分野と先入観
・3872　接触角から起業まで

8/28（水）学習時間：5.75H
・橋本の物理（29）（30）
・フィラーの種類と特性についてマインドマップにまとめ
・TradosのマルチタームにExcelデータを流し込む方法を確認→できた

8/29（木）学習時間：6.25H
・比表面積測定法について調査
・0342　特許翻訳者が未経験分野を強みに変えるために

8/30（金）学習時間：5.25H
・比表面積についてまとめ、実際に計算
・0269　コンコーダンサー活用法
課題）
・細孔と表面張力、トリポーラスについて調べる
・サーマルプリンタについて調べ途中になっているので続き
・橋本の物理を進める